Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals3h 25m
0. Functions
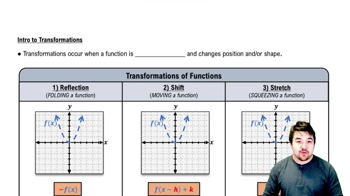
Transformations
Problem 53e
Textbook Question
Shifting and Scaling Graphs
Suppose the graph of g is given. Write equations for the graphs that are obtained from the graph of g by shifting, scaling, or reflecting, as indicated.
e. Stretch vertically by a factor of 5
 Verified step by step guidance
Verified step by step guidance1
Identify the original function g(x) that represents the graph you are working with.
To stretch the graph vertically by a factor of 5, you will multiply the entire function g(x) by 5.
Write the new equation as h(x) = 5 * g(x). This represents the vertical stretch.
Understand that this transformation will make all y-values of the graph 5 times larger, while the x-values remain unchanged.
Graph the new function h(x) to visualize the effect of the vertical stretch on the original graph g.
Was this helpful?

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice