Here are the essential concepts you must grasp in order to answer the question correctly.
Limit of a Function
The limit of a function describes the behavior of that function as the input approaches a certain value, which can be finite or infinite. In this context, the limit as t approaches infinity indicates how the function behaves as time progresses indefinitely. Understanding limits is crucial for analyzing the long-term behavior of dynamic systems, such as populations or physical processes.
Recommended video:
Limits of Rational Functions: Denominator = 0
Steady State (Equilibrium)
A steady state, or equilibrium, occurs when a system's variables remain constant over time, indicating that the system has reached a balance. In mathematical terms, this is often represented by the limit of a function equating to a constant value as time approaches infinity. Identifying steady states is essential in various fields, including biology and physics, to predict system behavior under stable conditions.
Recommended video:
Work Done On A Spring (Hooke's Law)
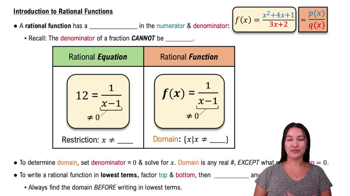
Rational Functions
A rational function is a ratio of two polynomial functions. In the given example, the population function p(t) = 3500t / (t + 1) is a rational function where the numerator and denominator are both polynomials. Analyzing rational functions involves understanding their limits, asymptotic behavior, and potential steady states, which are critical for determining the long-term behavior of the system they represent.
Recommended video:
Intro to Rational Functions
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47m