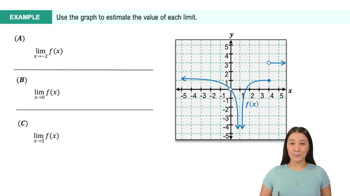
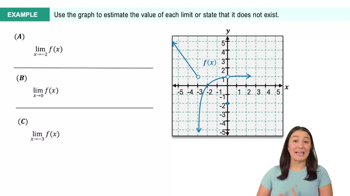
Determine whether the following statements are true and give an explanation or counterexample.


e. $\underset{x\to \frac{\pi }{2}}{\lim }\cot x=0$ . (Hint: Graph y=cot x)

Key Concepts

Limit of a Function

The limit of a function describes the behavior of that function as the input approaches a certain value. In this case, we are interested in the limit of the cotangent function as x approaches π/2. Understanding limits is crucial for analyzing the continuity and behavior of functions at specific points, especially where they may not be defined.

Cotangent Function

The cotangent function, denoted as cot(x), is the reciprocal of the tangent function, defined as cot(x) = cos(x)/sin(x). It is important to note that cot(x) is undefined at points where sin(x) = 0, such as x = nπ, where n is an integer. This characteristic affects the limit as x approaches π/2, where the function exhibits vertical asymptotic behavior.

Graphical Analysis

Graphical analysis involves examining the graph of a function to understand its behavior visually. For the cotangent function, plotting y = cot(x) reveals that as x approaches π/2, the function tends toward negative infinity, not zero. This visual representation helps clarify the limit's value and provides insight into the function's discontinuities and asymptotes.