Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
2. Intro to Derivatives
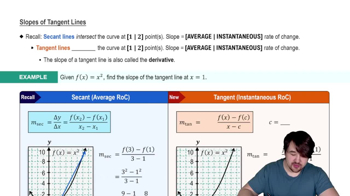
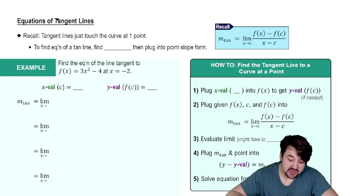
Tangent Lines and Derivatives
Problem 58
Textbook Question
Textbook Question{Use of Tech} Flow from a tank A cylindrical tank is full at time t=0 when a valve in the bottom of the tank is opened. By Torricelli’s law, the volume of water in the tank after t hours is V=100(200−t)², measured in cubic meters.
b. How long does it take for the tank to empty?
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Torricelli's Law
Torricelli's Law describes the speed of fluid flowing out of an orifice under the force of gravity. It states that the speed of efflux of a fluid through a hole is proportional to the square root of the height of the fluid above the hole. This principle is crucial for understanding how the volume of water in the tank changes over time.
Volume Function
The volume function V(t) = 100(200−t)² represents the volume of water in the tank as a function of time t. This quadratic function indicates how the volume decreases as time progresses, and analyzing this function helps determine when the tank will be empty, specifically when V(t) equals zero.
Recommended video:

Properties of Functions
Finding Roots of a Function
Finding the roots of a function involves determining the values of t for which the function equals zero. In this context, solving V(t) = 0 will provide the time it takes for the tank to empty. This process often involves algebraic manipulation and understanding the properties of quadratic equations.
Recommended video:

Finding Limits by Direct Substitution

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice