Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
Problem 2.1.19
Textbook Question
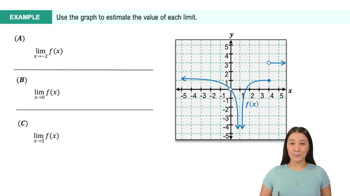
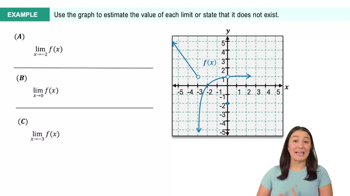
Textbook QuestionConsider the position function s(t)=−16t^2+100t. Complete the following table with the appropriate average velocities. Then make a conjecture about the value of the instantaneous velocity at t=3. <IMAGE>
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
12mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Position Function
A position function describes the location of an object at a given time. In this case, s(t) = -16t² + 100t represents the height of an object in free fall, where 't' is time in seconds. Understanding how to interpret this function is crucial for analyzing motion and calculating velocities.
Recommended video:

Relations and Functions
Average Velocity
Average velocity is defined as the change in position over the change in time, calculated as (s(t2) - s(t1)) / (t2 - t1). It provides a measure of how fast an object is moving over a specific interval. Completing the table with average velocities helps in understanding the object's motion between different time points.
Recommended video:

Derivatives Applied To Velocity
Instantaneous Velocity
Instantaneous velocity is the velocity of an object at a specific moment in time, found by taking the derivative of the position function. It represents the object's speed and direction at that exact time. Making a conjecture about the instantaneous velocity at t=3 involves evaluating the derivative of the position function at that point.
Recommended video:

Derivatives Applied To Velocity

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning