Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
2. Intro to Derivatives
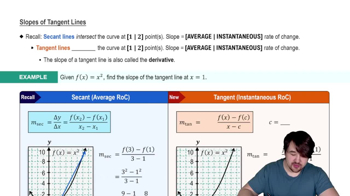
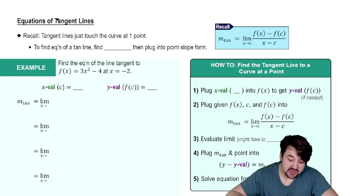
Tangent Lines and Derivatives
Problem 45
Textbook Question
Textbook QuestionAverage and marginal profit Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x) = xp(c) - C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/x and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item, given that x items have already been sold. Consider the following cost functions C and price functions p.
a. Find the profit function P.
C(x) = − 0.04x²+100x+800, p(x)=200, a=1000
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Profit Function
The profit function P(x) represents the difference between total revenue and total costs when selling x items. It is calculated as P(x) = xp(x) - C(x), where xp(x) is the total revenue from selling x items at price p(x), and C(x) is the total cost of producing those items. Understanding how to derive this function is crucial for analyzing profitability.
Recommended video:

Example 3: Maximizing Profit
Average Profit
Average profit is defined as the profit per item sold, calculated by dividing the total profit P(x) by the number of items sold, x. This metric provides insight into the profitability of each item and helps in assessing overall performance. It is expressed as Average Profit = P(x)/x, which simplifies the analysis of profit distribution across units sold.
Recommended video:

Example 3: Maximizing Profit
Marginal Profit
Marginal profit refers to the additional profit gained from selling one more unit of a product, represented mathematically as the derivative of the profit function, dP/dx. This concept is essential for understanding how profit changes with small variations in the quantity sold, allowing businesses to make informed decisions about production levels and pricing strategies.
Recommended video:

Example 3: Maximizing Profit

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice