Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Introduction to Functions
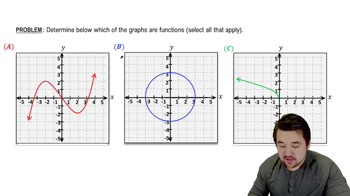
Problem 112c
Textbook Question
Daylight function for 40 °N Verify that the function D(t)=2.8sin(3652π(t−81))+12 has the following properties, where t is measured in days and D is the number of hours between sunrise and sunset.
and (corresponding to the equinoxes).
 Verified step by step guidance
Verified step by step guidance1
First, understand the function D(t) = 2.8\sin\left(\frac{2\pi}{365}(t-81)\right) + 12. This function models the number of daylight hours as a sinusoidal function of time, where t is the day of the year.
To verify the property D(81) = 12, substitute t = 81 into the function: D(81) = 2.8\sin\left(\frac{2\pi}{365}(81-81)\right) + 12. Simplify the expression inside the sine function.
Notice that \sin(0) = 0, so the expression becomes D(81) = 2.8 \times 0 + 12 = 12. This confirms that D(81) = 12, which corresponds to the spring equinox.
Next, verify the property D(264) \approx 12. Substitute t = 264 into the function: D(264) = 2.8\sin\left(\frac{2\pi}{365}(264-81)\right) + 12. Simplify the expression inside the sine function.
Calculate \frac{2\pi}{365}(264-81) and find the sine of this angle. Since the sine function oscillates between -1 and 1, the value of D(264) will be close to 12, confirming the property for the autumn equinox.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Was this helpful?

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Callie
Start learning