Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
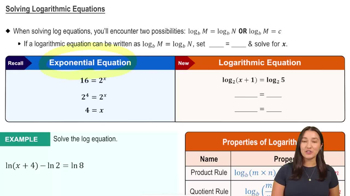
Exponential & Logarithmic Equations
Problem 13
Textbook Question
The parabola y=x²+1 consists of two one-to-one functions, g₁(x) and g₂(x). Complete each exercise and confirm that your answers are consistent with the graphs displayed in the figure. <IMAGE>
Find formulas for g₁((x) and g₁⁻¹(x). State the domain and range of each function.
 Verified step by step guidance
Verified step by step guidance1
<strong>Step 1:</strong> Identify the one-to-one functions from the parabola \( y = x^2 + 1 \). Since a parabola is symmetric about its vertex, we can split it into two functions: one for the left side and one for the right side. For the right side, where \( x \geq 0 \), the function is \( g_1(x) = x^2 + 1 \).
<strong>Step 2:</strong> Determine the inverse of \( g_1(x) \). To find \( g_1^{-1}(x) \), start by setting \( y = x^2 + 1 \) and solve for \( x \). Rearrange to get \( x^2 = y - 1 \), then take the square root: \( x = \sqrt{y - 1} \). Thus, \( g_1^{-1}(x) = \sqrt{x - 1} \).
<strong>Step 3:</strong> State the domain and range of \( g_1(x) \). Since \( g_1(x) = x^2 + 1 \) and we are considering \( x \geq 0 \), the domain of \( g_1(x) \) is \([0, \infty)\). The range is \([1, \infty)\) because the smallest value of \( x^2 + 1 \) is 1 when \( x = 0 \).
<strong>Step 4:</strong> State the domain and range of \( g_1^{-1}(x) \). The domain of \( g_1^{-1}(x) = \sqrt{x - 1} \) is \([1, \infty)\) because the expression under the square root, \( x - 1 \), must be non-negative. The range is \([0, \infty)\) because the square root function outputs non-negative values.
<strong>Step 5:</strong> Verify consistency with the graph. Check that the domain and range of \( g_1(x) \) and \( g_1^{-1}(x) \) match the sections of the parabola and its inverse on the graph. Ensure that \( g_1(x) \) covers the right side of the parabola and \( g_1^{-1}(x) \) reflects this section across the line \( y = x \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
One-to-One Functions
A one-to-one function is a function where each output is produced by exactly one input. This means that if f(a) = f(b), then a must equal b. For the parabola y = x² + 1, it is not one-to-one over its entire domain, but can be restricted to intervals where it is, allowing for the definition of inverse functions.
Recommended video:

One-Sided Limits
Inverse Functions
An inverse function essentially reverses the effect of the original function. If g(x) is a function, then its inverse g⁻¹(x) satisfies the condition g(g⁻¹(x)) = x for all x in the domain of g⁻¹. To find the inverse of a one-to-one function, you typically swap the x and y variables and solve for y.
Recommended video:

Inverse Cosine
Domain and Range
The domain of a function is the set of all possible input values (x-values) that the function can accept, while the range is the set of all possible output values (y-values) that the function can produce. For the functions g₁(x) and g₂(x) derived from the parabola, understanding their domains and ranges is crucial for accurately defining their behavior and ensuring the validity of their inverses.
Recommended video:
Finding the Domain and Range of a Graph

 4:46m
4:46mWatch next
Master Solving Exponential Equations Using Like Bases with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice