Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
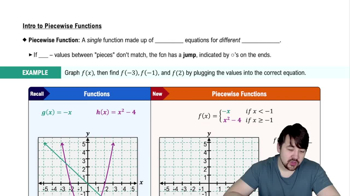
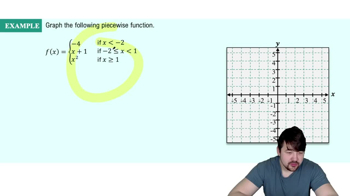
Piecewise Functions
Problem 28
Textbook Question
Taxicab fees A taxicab ride costs $3.50 plus $2.50 per mile for the first 5 miles, with the rate dropping to $1.50 per mile after the fifth mile. Let m be the distance (in miles) from the airport to a hotel. Find and graph the piecewise linear function c(m) that represents the cost of taking a taxi from the airport to a hotel m miles away.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem by identifying the different cost components for the taxi ride. The initial cost is $3.50, and the cost per mile changes after 5 miles.
Step 2: Define the piecewise function c(m) for the cost. For the first 5 miles, the cost is $3.50 plus $2.50 per mile. For distances greater than 5 miles, the cost is $3.50 plus $2.50 per mile for the first 5 miles, and $1.50 per mile for any additional miles.
Step 3: Write the piecewise function c(m). For 0 <= m <= 5, c(m) = 3.50 + 2.50m. For m > 5, c(m) = 3.50 + 2.50*5 + 1.50*(m - 5).
Step 4: Simplify the expression for m > 5. Calculate the cost for the first 5 miles and then add the cost for the additional miles.
Step 5: Graph the piecewise function. Plot the linear segment for 0 <= m <= 5 and the linear segment for m > 5, ensuring continuity at m = 5.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Related Videos
Related Practice