Intro to Extrema - Online Tutor, Practice Problems & Exam Prep

Finding Extrema Graphically

In the past, we've identified the extrema on a graph. These are our maximum and minimum values that occur at the highest and lowest points of a function, but there's actually a bit more to it than that because there are two different types of extrema. There are global extrema, which are the highest and lowest points of the entire function, and local extrema, which are the highest and lowest points when considering just part of a function. Now, I'm going to walk you through the difference between these two types of extrema and show you exactly how to identify them on a graph. So let's go ahead and get started.

Now, in our example here, we are asked to determine whether each labeled point is a global max or min, a local max or min, or none at all. So let's start by talking about global extrema. You may hear global extrema referred to as absolute extrema, but just know that this means the same thing. Remember that earlier, I mentioned that global extrema mean we are considering the entire function. So let's get a bit more specific here.

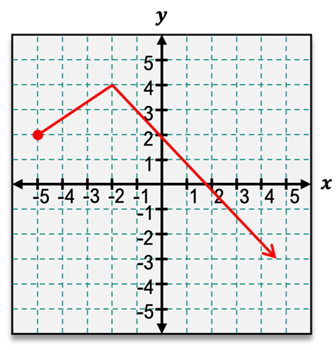
We're going to be working with this x value c here. And if we plug c into our function, so we get f(c), if f(c) is then greater than or equal to f(x) for all other x values of our function, that means that this point represents a global maximum. On a graph, that just means that if we look at the entire function, our highest point of that whole function is our global maximum. Looking at this function specifically, I can see that my highest point is right here. So this point is my global maximum.

There are a couple of different ways that I could state this as an answer. I could express this as an ordered pair and say that my global maximum of my function is located at negative 35. Or I could also say that my function reaches a global maximum value of 5 at x equals negative 3. Both of these would be correct answers. Now, that was our global maximum, but let's look at our global minimum.

If f(c) is instead less than or equal to f(x) for all x, that point is then a global minimum. On a graph, remembering that we look at the entire function because we're working with global extreme values, for a global minimum, this is going to be our lowest point of our entire function. And for this function specifically, I can see that that happens right here at negative 5, negative 5. So this point is my global minimum. For our global extrema, we want to look at our entire function and identify our highest and lowest points.

Now let's shift to our local extrema. You may also hear local extrema referred to as relative extrema. But again, this means the same thing. Now for global extrema, we are looking at the whole function. For local extrema, we are now looking at just part of it.

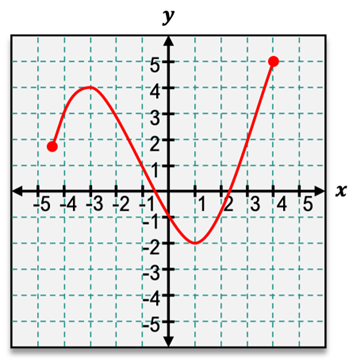
But what do I mean by that? Well, if we're looking at a local maximum, then f(c) is going to be greater than or equal to f(x) but for all nearby x. So instead of for all x like for our global maximum, this is just for all x nearby because it's just a local maximum. Now what does this look like? Well, coming over to our graph here, if I were to zoom in on this little region of my graph, I can see that this point at 24, we are higher than all those nearby points.

So this point is a local maximum. Now what about our local minimum? Well, for our local minimum, this is going to be where f(c) is less than or equal to f(x), again, just for all nearby x values. So again, coming over here to our graph, if I zoom in on this little region here, I can see that we formed this little valley where this point 1 is. And it is lower than all those nearby points on my graph.

So that means that this point is a local minimum. Our local extrema are just our highest and lowest points within a small region. These typically look like the peaks and valleys that we see on our graph here. Now that we've looked at both global and local extrema, some points may actually be both a global value and a local value. So what does that look like?

Well, if we come back over here to our global maximum and if we zoom in just on that particular region and look directly around it, we can see that this point, negative 35, is higher than all of those nearby points. That means that this point is not only a global maximum but also a local maximum because it's not only the highest point of our entire function but it's also the highest point in just this particular region. Now if our global maximum is also a local maximum, what about our global minimum? Well, since our global minimum is actually the endpoint of our function here, things are going to get a bit more complicated. This is one of those things that in math not everyone agrees on, so we have to choose a convention to use.

Now by the convention that we are going to use here in this course, endpoints can be global extrema. Like here, this endpoint is our global minimum. But they cannot be local extrema, meaning that this endpoint cannot also then be a local minimum as well as a global because it's an endpoint. And when looking at our other endpoint here, we know that this is not a global max or min because it's not the highest or lowest value of our entire function, but it also cannot be a local max or min specifically because it's an endpoint. Remember that this is something that can vary between your textbook or professor, so be sure to verify what convention you should use in your coursework specifically.

Now that we know what global and local extrema are and how to identify them on a graph, let's get more practice together. I'll see you in the next one.

Finding Extrema Graphically Example 1

In this problem, we're asked to identify the extreme values of the function \( f(x) \) on the specified domain. Now, this is actually the same exact function in all of these graphs. The difference is the domain over which this function is defined. Let's go ahead and start all the way over on the left here with our first graph. This function is defined over the domain of all real numbers from negative infinity to positive infinity.

So, what extreme values, what global maxes and mins or local maxes and mins does this function have? Well, looking at this function, I can see that the absolute lowest point of my graph is down here at \( x = 0 \). Now, because this is the lowest point on my function, I can say that this is a global minimum. Also, because this point is not an endpoint and I can kind of zoom in here, I can see that this is the lowest point compared to all nearby points. So, this is not only a global minimum, but it is also a local minimum.

We have a global and local minimum of \( f(0) = 0 \) at \( x = 0 \). Now, when thinking about maximum values, looking at this function, since it's defined from negative infinity to positive infinity, I can see that my graph continues to go up to infinity on both sides of this function, meaning that there's not one single maximum value that this function reaches. So there are no maximum values for this function; there's only a minimum.

Let's move onto our next graph. Here, we have the same function but now defined over the domain from 0 to 3 with both of those endpoints, 0 and 3, included in that domain. So, what are our maximum and minimum values here? Well, I can see that my very lowest point on my function is here at \( x = 0 \). So this point represents my global minimum.

Now you may be thinking here, is this also a local minimum? But remember, because of the convention that we are using here in this course, endpoints cannot be local extrema. So this point is only a global minimum. We have our global minimum of \( f(0) = 0 \) at \( x = 0 \). Now, remember that this is something that may vary between your textbook or professor.

So, again, be sure to verify what convention you should use when it comes to considering endpoints as local extrema. Now what about the other side of our function here? I can see that this very highest point happens here at \( x = 3 \). So this is again an endpoint. It can't be a local maximum, but it can be my global maximum, and it is because it's that very highest point. So this function has a global maximum of \( f(3) = 9 \) at \( x = 3 \).

So this function has both a global minimum and a global maximum, but no local extrema because those endpoints were my global min and max. Now moving on to our last function here. Here, we see that our domain is defined from 0 to 3, but this time, my endpoints are not included in that domain. So what are our extreme values of this function? Well, when we think about reaching the very lowest point, that would be our global minimum, we would think about this point here at 0.

But this point is not included in our domain. So, we can't say that that's where our global minimum is. Now you may be thinking, well, couldn't our global minimum be at 0.01 or 0.001? And to that, I would say, well, what about 0.0001? That's exactly the problem that we're encountering here. We can get closer and closer to 0, but we can never quite reach it.

And there's always going to be a value on our function that is smaller than whatever we're thinking of. Even if I said 0.0001, you could still get smaller. So there are no local or global extrema on this function because we come to the same conclusion when looking at this other point. We could say, okay. Well, we could get to 2.99 or 2.999 to get to that maximum value.

But remember that you can always get a higher value because we can't ever reach that endpoint because it's not included in our domain. So for this last function here, there are no extreme values that we can identify. So looking at these functions, we can see that even though they're all the same exact function, because they're defined over different domains, our extreme values look completely different. Now, be sure to keep this in mind as we continue practicing. I'll see you in the next one.

Finding Extrema Graphically Example 2

In this problem, we're asked to label where the local and global maxima and minima occur on the graph of this function f(x). So let's go ahead and dive in. Now looking at our function here, remember that maxes and mins are most often going to occur where there are these sorts of peaks and valleys that we see happen. So let's go ahead and take a look at a couple of these points. Now looking at my function as a whole, I can see that the very highest point of this entire function is right here at x equals negative 2.

Now because this is the highest point of my entire function, that tells me that this is my global maximum. But, again, if I were to zoom in on this point, I can see that it's also the highest point of those points nearby. So this is not only a global maximum but also a local maximum. Now this will pretty much always happen unless your global max or min is at an endpoint.

So let's keep going here. Now that was our highest point of our entire function. We also want to take a look at our very lowest point of our function, which I can see happens here at x equals 1. So that tells me that this point is my global minimum. And remember, if I were to zoom in here, it's also the lowest point of all those nearby.

So this is both a global and a local minimum. Now we want to find if there are any other local maxes and mins. There can't be any other globals because we already have our absolute highest and lowest points, but there can, of course, be more local points. I want to take a look at all of these little peaks and valleys that happen.

So over here at x equals negative 4, I can see this little valley forming. And if I were to zoom into this point here, I can see that it is the lowest point of all those nearby points. So this is a local minimum. Now shifting over to this side of my graph over here, I can see that my function's graph is reaching a sort of peak here at x equals 3. So that tells me that, zooming in here, I can see that this is the highest point of all those nearby points.

This point is a local maximum. Now I see this valley forming down here at x equals 5, again cluing me in that this is a local minimum. If I zoom into just that point, I can see it's lower than all of my nearby points. This point is a local minimum. Now something you may be wondering here is, what about those endpoints?

Remember that based on the convention we will use in this course, endpoints cannot be local extrema. And because these are not global extrema or endpoints, they're actually not extreme values at all. So here, we've identified all of our local and global maxima and minima. Feel free to let me know if you have questions, and let's keep practicing.

Determine where the local and absolute maxima and minima occur on the given graph of $f\left(x\right)$.

• A. Absolute max of 4 at $x=-2$, Absolute min of $-3$ at $x=5$
• B. Absolute max of 4 at $x=-2$, Local max of 4 at $x=-2$, No absolute or local mins
• C. Absolute max of 4 at $x=-2$, Absolute min of 2 at $x=-5$
• D. Absolute max of 4 at $x=-2$, Local max of 4 at $x=-2$, Local min of 2 at $x=-5$

Determine where the local and absolute maxima and minima occur on the given graph of $f\left(x\right)$.

• A. Absolute max of 5 at $x=4$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$ & 1.5 at $x=-4.5$
• B. Absolute max of 5 at $x=4$, Absolute min of $-2$ at $x=1$, No local extrema
• C. Absolute max of 4 at $x=-3$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$
• D. Absolute max of 5 at $x=4$, Local max of 4 at $x=-3$, Absolute min of $-2$ at $x=1$, Local min of $-2$ at $x=1$$x=1$

Finding Extrema Graphically Example 3

If you haven't already, go ahead and try to solve this problem on your own before checking back in with me. Let's dive in here. Now, we are asked to sketch a graph of a function that is continuous over the interval from negative 3 to 2, both of those endpoints included. It has the properties listed below: an absolute maximum at x=2, an absolute minimum at x=0, and a local maximum at x=−2. Keep in mind that if you already tried this on your own, your function might look a little different than mine because we can still have different features as long as we maintain all of these absolute and local maxima and minima, with our endpoints the same. So, let's start sketching our graph here.

I know that I must have endpoints at negative 3 and 2, and I know that those endpoints will be solid dots because those points are included in that interval. We're told that we have an absolute maximum at x=2, which is also one of our endpoints. This needs to be the highest value that my function reaches as it's an absolute maximum. I'm going to place my absolute maximum somewhere up here. It doesn't matter where, as long as it's the highest point of the entire function.

Then, we have an absolute minimum, which is the lowest point of the entire function, at x=0. I will place this point somewhere down here on my graph. Since this is not an endpoint, it will likely appear as a valley. Finally, we have a local maximum at x=−2. This means that I need to mark a peak at this point, ensuring it does not exceed the absolute maximum.

The final point to include is the endpoint at negative 3. This is not considered an extremum. I will place it here on my x-axis and will then connect our function. Being continuous, there should be no breaks or holes. I will connect each segment smoothly: rise up to the absolute maximum, then plummet down to the valley, and finally ascend to the absolute maximum at x=2.

To verify, our graph includes everything needed: endpoints at negative 3 and positive 2, an absolute maximum at x=2, an absolute minimum at x=0, and a local maximum at x=−2. The graph correctly portrays a peak that is higher than nearby points but is not the highest point of the entire function. I've successfully sketched my graph here. Let us know if you have any questions, and let's keep working.