Basic Graphing of the Derivative - Online Tutor, Practice Problems & Exam Prep

Graphing The Derivative

At this point in the course, we should be familiar with what a derivative is, and how a derivative relates to something known as the tangent line. These are both things that we've learned about in previous videos. Now in this video, we're going to be talking about situations that you're going to see in this course where you are given the graph of some function f(x), and you will need to sketch the derivative of that graph simply based on what the function looks like. This might sound like something that's totally scary or abstract, but don't sweat it because in this video, I'm going to be walking you through an example of this type of problem. And I think you're going to find that if you can relate the derivative to the idea of a tangent line, then solving these types of problems actually becomes pretty straightforward.

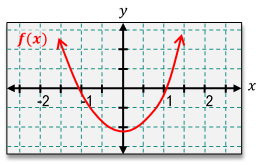
So without further ado, let's just jump right into things to see what an example of this would look like. In this problem, we are told for each x value or interval, determine if the slope of f(x), our function, is positive, negative, 0, or undefined, and then sketch the derivative f'(x). Now that's a lot just when we hear all those words, but let's take this step by step. Our first step is going to be to understand how this function in general behaves, and what the tangent lines are going to look like based on this function. Recall that the derivative is the exact same thing as the slope of a tangent line.

Wherever we find the slope of a tangent line, that's going to be what the derivative value is at that specific point. Of course, what we could do to graph the derivative is literally just fill this curve with a bunch of points, and find a bunch of tangent lines at every single point and write each one out. But that would take a lot of time because we could draw millions of points on this graph and millions of tangent lines, and that would just take forever. So it's not the most efficient way of solving these types of problems. But, again, if you understand the general behavior of these functions, then you can actually understand this and graph it in a much more efficient way.

Now let's go ahead and start by just taking a look at what this graph does as we go from left to right. And the way that I like to solve these types of problems is to imagine there's a person literally standing on this graph, and they're walking from left to right. We're going to first focus on this portion of the interval, which is negative infinity all the way down here, all the way up to negative one. So it's going to be at that point. How is this function going to be behaving as this person walks from left to right all the way to negative one?

Well, as this is happening, notice the person is going uphill. So you could say that the function is increasing. Now whenever the function is increasing, notice anytime we draw a tangent line here, the tangent line is going to have a positive slope. And you can see that the derivative is going to be positive where the function is increasing. But what would happen as this person walked all the way up this hill and got to this point right here? We'll notice at this point, if we draw a tangent line, it's going to be completely flat. So we would get a horizontal tangent line, and the slope of any kind of horizontal or flat line is always going to be 0. So at this point, negative 1, the derivative is going to be 0. But now let's see what happens as we go to this next interval, which goes from negative one all the way over here to positive one. Well, at this interval, notice how a person would be walking downhill.

And because they're walking downhill, we could see that the function decreases. And when the function decreases, the slope of the tangent lines are all going to be negative, because notice how they slope down now instead of up. So we're going to have a negative derivative from this interval. So this is something that's important to recognize. Whenever you have a situation where your function is increasing, the derivative is going to be positive. However, if it's decreasing, the function is going to be negative. And whenever you see a situation where you have a horizontal tangent line or you're basically flat, that means that your derivative is going to be 0. So this is the behavior that you need to understand when looking at a graph of some function.

Now we're going to take a look next at this point right here at positive one. Notice once again, we can get a horizontal tangent line right there. So because we get another flat line, the derivative is going to be 0. Now lastly, we'll take a look at this final interval from 1 to positive infinity, and notice at this point, the person is going to be going uphill. Because they're going uphill at this entire interval, that means that the derivative here is going to be positive because the function is increasing. So we've basically solved this entire portion of the problem, but now the question becomes, how exactly could we use all of this information to sketch what the derivative looks like? The way that we can do this is by first finding the obvious points on our graph.

In my opinion, the obvious points are always going to be where we have these flat tangent lines, because that's going to be where the slope is 0. So if I know that my derivative is 0, that means that it's literally touching the x-axis. So notice that we have a flat tangent line here and there. Whenever you have these peaks and valleys in your graph, the tangent lines are going to be flat. What I can do is I can draw this point to be right there, right on the x-axis, and I can draw this point to be right here on the x-axis. Because, again, the y values are going to be 0 because the derivative is 0 at those points. Now notice here, we said that the derivative is positive, and that's going to be on this whole interval, which on our graph here is going to correspond to this whole interval. So what that means is that if we are positive, that means it's going to be some value above the x-axis where the outputs would be positive. Now notice at this interval right here, we said that we have a negative derivative. And because our derivatives are negative, that means somewhere here we're going to be below the x-axis.

Then we can see for this last interval, the derivatives are positive, which means that we're going to be again above the x-axis. Now what I can see at this part of the interval is these tangent lines are going to get closer and closer to flat until we reach this point where we actually are flat. So that means that we're going to start above the x-axis, and we're gonna get closer and closer to the x-axis until we reach that point. Now what I can see for this region is that the tangent lines start flat, and then they slope down, and then they go flat again. So that means they're going to dip below th

Based on the graph $f\left(x\right)$, describe the graph of the derivative $f^{\prime}\left(x\right)$ on the interval $\left(0,\infty\right)$.

• A. Below the x-axis
• B. Above the x-axis
• C. On the x-axis

Based on the graph $f\left(x\right)$, describe the graph of the derivative $f^{\prime}\left(x\right)$ at the point $x=-1$.

• A. Above the x-axis
• B. Below the x-axis
• C. On the x-axis

Based on the graph $f\left(x\right)$, describe where the derivative curve $f^{\prime}\left(x\right)$ would be below the x-axis.

• A. (-$\infty$,-1) U (0,1)
• B. (-1,0) U (1,$\infty$)
• C. (-$\infty$, -1) U (1,$\infty$)
• D. (-1,1)

Graphing The Derivative Example 1

Welcome back, everyone. In this example, we're told given the function \( f(x) \), sketch the derivative of the function \( f'(x) \). This is an example where we have to sketch the derivative based on the function that we have. Recall that the way we do this is by looking at the behavior of the tangent lines and the curve in general to see what the function is going to look like when we take its derivative. So let's go ahead and get started. I see that we have this function \( f(x) \), a function that oscillates up and down.

It kind of looks like a sine wave, actually. You could just look up what the derivative of a sine wave looks like, but I think it's going to be better if we use our intuition and the concepts we've learned to graph this. First, I like to start these problems by finding all the places where the derivative would be 0, or the slope, I should say. The way I can do this is to find any place where I can draw a flat tangent line. That's going to be at any of these kind of peaks or valleys on your graph.

From here, I can see that these are going to be all the places where these flat tangent lines occur. Because of this, these are all the places where these slopes are going to be 0. And remember, wherever the slope of the tangent line is 0 on the derivative graph, that is going to be a point on the x-axis. There is a point right here between negative two and negative one, which would be about negative 1.5. We have another point right here and another point right there.

On our derivative graph, this would be a point on the x-axis. This is where the derivative here touches or crosses the x-axis. Next, I need to figure out how the tangent lines behave as we go from left to right. Starting by looking at the left part of the graph before we get to the flat tangent line, any tangent line I draw is going to be positive. Because it's a positive slope, it's going to be above the x-axis. We have increasing tangent lines with positive slopes, meaning we're going to be somewhere up here, above the x-axis.

Then, if I go to the right of this flat tangent line, we're going to have a negative slope, meaning we're going to be below the x-axis. Notice how these tangent lines will continue to have a negative slope until we get to this point right here. Since this slope is going to flatten out, it's going to start to come back up, less negative basically. Then when I get to right here, that's another flat point, meaning we're going to come back up here to the x-axis. From here to there, we have positive slopes tangent lines, so we're going to be above the x-axis.

I can see that these positive slope tangents are going to get less and less steep as we get close to this point, so we're going to start coming closer to the x-axis again until we touch it right about there. Then we have some negative tangent lines, which are going to get less negative as we get to this flat point, so it's going to be below the x-axis till we get to this next point. Then once again, we have these positive slopes, and we are going to be above the x-axis again. So the curve is going to look something like this, and that is our derivative function.

The funny thing about this curve is this is actually the function for a cosine. We had a sine looking wave over here, and we get a cosine looking wave over there. So we can conclude that the derivative of the sine is a cosine based on this graphing method here. But since we weren't directly given that this is a sine function or that this is a cosine function, we've used this method to depict what the curve is going to look like as its derivative. This would be the solution over here.

This is the graph, and that is how you can solve these types of problems. I hope you found this video helpful. Let's move on.

Graphing The Derivative - Special Cases

So at this point, we should be familiar with how we can graph the derivative of a function, but it turns out in this course, not all of the graphs that you're going to see are going to be these nice kind of curves where we can easily see how the tangent lines behave. Instead, we're often going to see these types of situations where we have these graphs that are kinda weird looking. Notice how we have some sharp turns, and we have these jumps, and these are what we refer to as special cases. Now this might sound a bit scary, but don't sweat it because I'm going to walk you through how you can solve these types of problems where you need to graph the derivative. And it turns out it's actually very similar to how we graphed regular situations, ordinary functions.

There are just a couple extra rules we need to know. So let's go ahead and get right into things. Now the same way that we went with graphing derivatives of functions, we can use the same process on these special cases. We can just imagine that there's a little person on this graph here, and they're walking from left to right. Now notice for this first interval, if we take a look at how this person behaves, they're going to be going across this flat line.

We know anytime we see these horizontal lines, that means that the derivative is 0. So that means this whole portion of the graph right here is just going to be on the x-axis because the derivative of any flat line or constant is 0. So this is what our graph is going to look like for this first portion. Now, what I'm going to do is jump over to this next portion here. Notice that we would have the same person, but now they would be going downhill.

That means that the graph is decreasing for this interval. And because the graph is decreasing on this interval, that means our derivative is going to be below the x-axis because we have a negative downward slope here. Now notice that we have a straight line. This is just a straight line here, and recall that the slope of any line is constant. So that means if we go here to our derivative graph, that this derivative is going to be some constant.

So this is what our function looks like so far. But notice here that we actually have this transition point that we haven't addressed yet, which is negative one. What exactly is happening right here? This is kind of tricky because we have a sharp turn, a sharp corner that happens right there. So what is this going to look like?

Is there going to be some way we can connect these points here? Is there something going on? Well, this is one of the rules that you need to know when dealing with these special cases. Whenever you have a discontinuity or some kind of sharp corner in your graph, that means that the derivative is not going to exist. And whenever the derivative does not exist, then there's going to be a jump in your graph.

So going right here, there's going to be a hole here and a hole there because the derivative function does not exist at that transition point because we have a sharp corner. So that's something you need to remember when dealing with these types of functions. If there's a sharp corner, the derivative does not exist. But now let's move to this next portion of the graph here, which looks something like this. Notice we would have this same person walking across the graph, then they'd have to kind of jump to get down to here.

Now what I can see here is that this function in general seems to kinda be increasing, which means that our derivative function is going to be above the x axis. But what exactly is this function going to look like? Well, what I can see here is that the tangent lines, if we look at this curve, would be relatively flat at that point. Then what I can see here is they start increasing as we get to this middle section, and then we start to get these really steep tangent lines. And then all of a sudden, they start to kind of flatten out when we get to the top of the curve again.

So where we have flat tangent lines, we know that the derivative is about 0 at that point, so that's gonna be where we start on the graph. Then as we go to the right, we can see that this person is going to be walking uphill which means it's going to be more increasing. So we'll hit this kind of peak as we go up here, and then it starts to flatten out again, which means we go back down to the x-axis. So we're going to have a curve that looks something like this. But once again, there's something else we need to address here, and that's going to be this transition point of 0.

Because notice right here, we have another transition where we have a jump. Because we have this jump right here, this is what's called a discontinuity. And at discontinuities, the derivative does not exist. So whenever we have these kinds of jumps or some sort of discontinuity, the derivative once again does not exist, which means our graph is once again going to have a jump at this point. So we'll have these two holes right here because the derivative does not exist there.

And that right there would be the graph of our function f' of x, and that is how you can sketch the derivative of this original function f of x. So this is how you can solve these types of problems where you have special cases. The main thing to remember is these two rules: whenever there's a sharp corner or a jump or some kind of discontinuity, the derivative does not exist. So I hope you found this video helpful, and let's go ahead and get some more practice.

Based on the graph $f\left(x\right)$, describe all points where the derivative $f^{\prime}\left(x\right)$ would have a jump.

• A. $x=-1.5$, $x=-1$, and $x=0.5$
• B. $x=-1$ and $x=0.5$
• C. $x=-1.5$
• D. Derivative $f^{\prime}\left(x\right)$ has no jumps

Graphing The Derivative - Special Cases Example 2

So here we have an example where we are told, given the function \( f(x) \), to sketch the derivative of the function \( f'(x) \). Let's see how we can go about solving this. Now, whenever I need to solve these problems where I need to sketch the derivative, I always like to start by figuring out all the places where we're going to touch the x-axis on the derivative graph. And that's going to happen whenever we can draw a line tangent to the curve that is flat, meaning it has a slope of 0. I can see one flat line I could draw, tangent to this curve, would be right there on this peak.

Whenever you have a peak or a valley in your graph, there's going to be a flat line that has a slope of 0. So that means that right here at negative 1.5, we're going to be touching the x-axis. Next, I can see we have a pretty long portion of the graph where the tangent line would be flat at every single point. So that means from negative one all the way over here to positive 1.5, we're going to have this flat line on our graph that touches the x-axis. So those are the places I see where we have tangent lines with a slope of 0.

There's no other place that I can draw a 0 slope tangent line, so that's going to be all the places we're touching the x-axis. So now I just need to construct the rest of this graph. If I start from left to right, I'm going to focus on this portion of the graph right here until we get to the 0 tangent line, the 0 slope tangent line, and what I can see is any line that I draw that's tangent to the curve right here is going to have a positive slope. So that means we're going to be above the x-axis at negative 2, and any place that is on this interval.

Next, what I can see is if I look at this next portion of the graph, we'll notice any tangent line I draw here would be negative. It would slope down. So because of this, we're going to be below the x-axis. This allows me to see that this is going to be a straight line, which looks something like this. We're going to have a straight line. It does have a slope to it because we can see that we have some sort of increasing and decreasing tangent lines, but that is going to be this portion of the graph.

This next portion of the graph right here, we have already sketched in. But what exactly happens at this point? Well, at that point, notice there's a sharp corner, and whenever we have these sharp corners, that is going to be a jump discontinuity. So at this point right down here, we're going to put an open circle because the graph is discontinuous right there for our derivative. Next, I can see that we stop right here at 1.5, and that's another sharp turn we have. Because we have another sharp turn, that means there's going to be another jump.

For this last portion of the graph, I can see that we have a line. This line has a certain slope to it, but the tangent line that we draw to this curve, the slope of this tangent line would be constant. So that means every place here that we see on our derivative graph is just going to be a constant. So we're going to have another line right here which goes forever in this direction, and it's going to be flat because this is a line with a constant slope.

This right here is how you can construct the derivative graph, and this would be the solution to this problem. This is how you can sketch these derivatives when you have these kinds of special cases with sharp corners or flat lines or even lines with a certain slope. I hope you found this video helpful. Thanks for watching, and let's move on.