Introduction to Limits - Online Tutor, Practice Problems & Exam Prep

Finding Limits Numerically and Graphically

Welcome back, everyone. Here, we're going to be taking our very first look at limits. The first time that you come across a limit, they may seem a bit intimidating. But in finding a limit, all we're doing is looking at what a function is doing around some given value of x. We can easily do this by either looking at a graph or by creating a table of values.

Now here I'm going to show you both of these ways of finding limits and we'll also walk through some of the notation that you'll encounter when dealing with limits. So let's go ahead and jump in here. First, let's take a look at our limit notation. This is what you'll see anytime you're working with a limit and we can read this as the limit of f of x, our function, as x approaches c, the value for which we're taking the limit. Now looking at this limit here, this is asking us to find the limit of x², that's our function f of x, as x approaches 2.

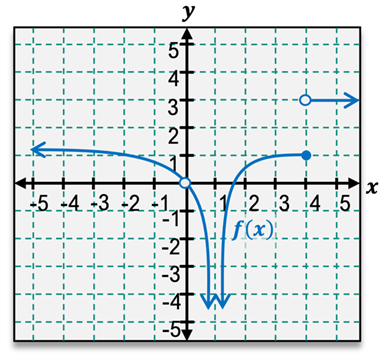
lim → x 2 x 2 = 4

Remember in finding a limit, we want to look at what our function is doing around that given value of x. A limit is the y value that a function f of x goes to as x gets really close to a given value. Here, we're looking for the y value that our function x² goes to as x gets really close to 2.

Looking at our graph, as x gets really close to 2 from either side, we want to see what y value our function is going to. First, looking at x from that left side closing in on 2, getting really close to it, I see that my function seems to be approaching a y value of 4. Numerically, plugging values that are getting really close to 2 into my function squaring them, here I get 3.96 and 3.996. Again, these values seem to be approaching a y value of 4. Now let's look at the other side. Plugging values into my function that are closing in on 2 from that other side, like 2.01 and 2.001. Plugging these values into my function, here I get 4.04 and 4.004. From this side, we see that we are indeed approaching a y value of 4.

So our limit of x² as x approaches 2 is 4. We used two different ways to find this limit: a table and a graph. Now let's work through a couple more examples together here.

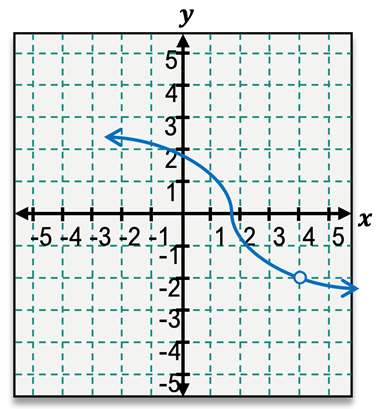
lim → x 1 ( x + 4 ) = 5

We want to find the limit of x+4 as x approaches 1 by creating a table of values. After looking at values really close to 1 from both sides and plugging them into our function, we can see that we are going to a y value of 5.

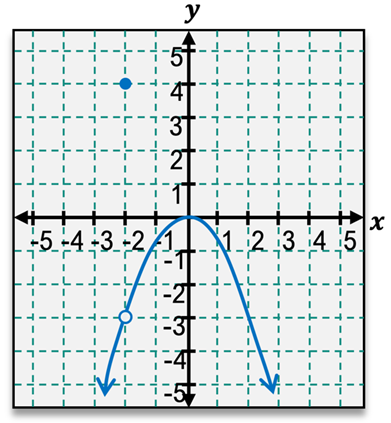
In some cases, we could have just plugged our c value into our function, like here, if we would have just plugged 1 into our function x+4, we would have gotten 5, which is exactly what our limit is. However, this is not always going to be true. We cannot always rely on plugging in that function value because our limit will not always be equal to the function value, so we can't just plug c in from the beginning. So with that in mind, let's look at this final example here. We want to find the limit of f of x as x approaches 3 using this graph.

lim → x 3 f ( x ) = 1

Looking at the graph, as x gets really close to 3 from both sides, we see that our function is going to a y value of 1. If we had just plugged 3 into our function or just looked at that function value on our graph, we would have gotten 4, which is a completely wrong answer. That is not what our limit is because our limit is 1. It's very clear that our limit will indeed not always be equal to our function value. We need to look at x getting really, really close to c, not x actually being equal to c because we never know if our function value is going to be something entirely different like we saw on our graph here or if it even exists at that point. It doesn't matter because we only care what's going on around it. So with this in mind, let's work through some more practice together.

Thanks for watching, and let me know if you have questions.

Find the limit by creating a table of values.

$\lim_{x\rarr0}-4x+2$

• A. $-4$
• B. $-2$
• C. $0$
• D. $2$

Find the limit by creating a table of values.

$\lim_{x\rarr2}3x^2+5x+1$

• A. $1$
• B. $10$
• C. $23$
• D. $21$

Find the limit by creating a table of values.

$\lim_{x\rarr1}\frac{x^2-4}{x-2}$

• A. $0$
• B. $3$
• C. $-3$
• D. $2$

Find the limit using the graph of $f\left(x\right)$ shown.

$\lim_{x\rarr1}f\left(x\right)$

• A. $2$
• B. $1$
• C. $0$
• D. Unable to determine

Find the limit using the graph of $f\left(x\right)$ shown.

$\lim_{x\rarr-2}f\left(x\right)$

• A. $4$
• B. $-2$
• C. $-3$
• D. Unable to determine

Find the limit using the graph of $f\left(x\right)$ shown.

$\lim_{x\rarr4}f\left(x\right)$

• A. $2$
• B. $-2$
• C. $0$
• D. Unable to determine

Finding Limits Numerically and Graphically Example 1

Hey, everyone. Make sure that you go ahead and try this example completely on your own before checking back in with me. But here, we're asked to use the graph to estimate the value of each of our limits here. Now the first limit that we're asked to find is the limit of f of x as x approaches negative 2. Now looking at our graph here, that tells us that we want to look at what our function is doing as x gets really, really close to negative 2 from either side.

So looking at our graph here, here is my x value of negative 2. And closing in on negative 2 from that left side, I see that my function seems to be approaching a value of 1. And also coming in from that right side, getting really, really close to negative 2, sort of closing in on it, I again see that my function seems to be approaching 1. So that tells me that my limit of f of x as x approaches negative 2 is equal to 1. Now let's look at our next limit here.

Here, we're asked to find the limit of f of x as x approaches 0. So again, we want to look at values really, really close to 0 from either side, sort of closing in on it. Now, on our graph here, if we approach 0, getting really, really close to it from that one side, I see that my function seems to be approaching a value of 0. Then coming in from the other side again closing in on that x value of 0, I again see that my function seems to be approaching a value of 0. So that's what my limit is.

Now, here, you might get tripped up by that hole in the middle of our graph because when x is 0, it seems like our function is not defined. There's a hole in our graph. But remember that it does not matter what the actual value of our function is at 0, just what it's doing as x gets really, really close to 0. So don't let that hole freak you out and go ahead and just remember that your limit is as x approaches 0, not when it is 0. Now let's look at one final limit here.

We're asked to find the limit of f of x as x approaches 3. Now looking at 3 on our graph here, wanting to close in on it from either side, our x value of 3 I see here coming from this left side, then my function seems to be approaching a value of 1. Then coming in from that right side, I see the same thing happening. My function is approaching a value of 1. So my limit of f of x as x approaches 3 is equal to 1.

Now, looking at this graph, you might already start to see that we have a sort of crazy thing happening over here. And if I would have asked you to find the limit as x approaches 4, you might get a little bit tripped up because from this side, I see that we're approaching 1. But from this side, we are not approaching 1. Now, I'm going to show you exactly how to deal with that coming up next in our next video. So I'll see you there.

Thanks for watching, and let me know if you have questions.

One-Sided Limits

When finding a limit, we look for the y value that our function is approaching as x gets really close to a given value from either side. Now, in looking at what our function is doing from either side of this x value, we've been finding what's called one-sided limits, which you may actually be asked to find explicitly. Since we've already been doing this, just not calling it one-sided limits, the only thing that's really new here is notation. Let's go ahead and jump right in. In working with a one-sided limit, we still write the limit of \( f(x) \), our function.

But instead of x just approaching \( c \), we have \( x \) approaching \( c \) with this little negative sign, indicating the left-sided limit. So we read this as the limit of \( f(x) \) as \( x \) approaches \( c \) from the left. For our right-sided limit, we have the limit of \( f(x) \) as \( x \) approaches \( c \) with a positive sign, indicating the right side. To remember which sign represents which limit, think about your coordinate system because we know that our x values from the left are negative, and our x values going to the right are positive.

Now that we've seen this notation, let's take a look at this function here and find some limits. Starting with our left-sided limit: the limit of \( f(x) \) as \( x \) approaches 3 from the left, as indicated by the negative sign. First looking at my graph here, as we get very close to 3 from the left side, I see that my function is approaching a y value of 1.

I can plug values that are getting very close to 3 from that left side into my function. As we're closing in on 3, I want to look at values like 2.999. Now because this is a piecewise function and these values are less than 3, my function here is equal to \( x - 2 \). So plugging these values into my function, here I get 0.999. Just like I saw on my graph, I can see here based on these values that my function is going to a y value of 1.

Thus, my left-sided limit, the limit of \( f(x) \) as \( x \) approaches 3 from the left is 1. Now let's take a look at our right-sided limit here, the limit of \( f(x) \) as \( x \) approaches 3 from the right. First looking at our graph, as we get really close to 3 from that side, I see that my function is going to a y value of 4. And again, I can look at those values that are getting close to 3 from that side, like 3.001, and again, plugging those into my function, which is just equal to 4 here. Based on these values, just like I saw on my graph, I can see that my function is going to a y value of 4.

My right-sided limit, the limit of \( f(x) \) as \( x \) approaches 3 from the right, is equal to 4. We found our one-sided limits from the left and from the right. But what if I now asked you to find the limit of \( f(x) \) as \( x \) approaches 3? Not from the left or from the right, but just as \( x \) approaches 3. This might be confusing because based on our one-sided limit, as \( x \) gets really close to 3 from either side, we see different things happening.

This tells us that because this function does not approach the same value from both sides, the limit does not exist, abbreviated as DNE. Now that we were able to find our one-sided limits, and because these one-sided limits were not equal to each other, that told us that our limit does not exist. So while you may be asked to explicitly find your one-sided limits, you may also be asked to use those one-sided limits to determine whether or not your regular limit exists or not. Let's go ahead and take a look at another example here. We want to use this graph to find the given limits.

The first limit we're asked to find here is the limit of \( f(x) \) as \( x \) approaches 1 from the left. So looking at my graph here, as \( x \) approaches 1 coming in from that left side, I see that my function is going to a y value of -1. So here, my left-sided limit is -1. Now let's move on to our next limit.

Here we have our right-sided limit, the limit of \( f(x) \) as \( x \) approaches 1 from the right. Now again, taking a look at our graph here, as \( x \) gets really close to 1 coming in from that right side, I see again that my function is going to a y value of -1. So here, my right-sided limit is the same as my left-sided limit, -1. Now let's look at one final limit here, the limit of \( f(x) \) as \( x \) approaches 1.

Since we already found our one-sided limits, and they are equal to each other, both being -1, that tells us that our limit here, the limit of \( f(x) \) as \( x \) approaches 1, is also -1, and we are done here. When working with one-sided limits, if they are not the same, then your limit does not exist. But if they are the same, then your limit does exist.

Now that we've seen and noted these one-sided limits and know how to use them to determine whether or not a limit exists, let's continue practicing. Thanks for watching, and I'll see you in the next one.

Using the graph, find the specified limit or state that the limit does not exist (DNE).

$\lim_{x\rarr-2^{-}}f\left(x\right)$, $\lim_{x\rarr-2^{+}}f\left(x\right)$, $\lim_{x\rarr-2^{}}f\left(x\right)$

• A. $\lim_{x\rarr-2^{-}}f\left(x\right)=1$, $\lim_{x\rarr-2^{+}}f\left(x\right)=1$, $\lim_{x\rarr-2^{}}f\left(x\right)=1$
• B. $\lim_{x\rarr-2^{-}}f\left(x\right)=1$, $\lim_{x\rarr-2^{+}}f\left(x\right)=-1$, $\lim_{x\rarr-2}f\left(x\right)=DNE$
• C. $\lim_{x\rarr-2^{-}}f\left(x\right)=1$, $\lim_{x\rarr-2^{+}}f\left(x\right)=1$ , $\lim_{x\rarr-2}f\left(x\right)=DNE$
• D. $\lim_{x\rarr-2^{-}}f\left(x\right)=0$, $\lim_{x\rarr-2^{+}}f\left(x\right)=0$, $\lim_{x\rarr-2}f\left(x\right)=0$

Using the graph, find the specified limit or state that the limit does not exist (DNE).

$\lim_{x\rightarrow0^{-}}f\left(x\right)$ , $\lim_{x\rightarrow0^{+}}f\left(x\right)$, $\lim_{x\rightarrow0}f\left(x\right)$

• A. $\lim_{x\rightarrow0^{-}}f\left(x\right)=0$, $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$, $\lim_{x\rightarrow0}f\left(x\right)=0$
• B. $\lim_{x\rightarrow0^{-}}f\left(x\right)=0$, $\lim_{x\rightarrow0^{+}}f\left(x\right)=0$, $\lim_{x\rightarrow0}f\left(x\right)=DNE$
• C. $\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$, $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$, $\lim_{x\rightarrow0}f\left(x\right)=DNE$
• D. $\lim_{x\rightarrow0^{-}}f\left(x\right)=-1$, $\lim_{x\rightarrow0^{+}}f\left(x\right)=-1$, $\lim_{x\rightarrow0}f\left(x\right)=-1$

Using the graph, find the specified limit or state that the limit does not exist.

$\lim_{x\rightarrow4^{-}}f\left(x\right)$, $\lim_{x\rightarrow4^{+}}f\left(x\right)$, $\lim_{x\rightarrow4}f\left(x\right)$

• A. $\lim_{x\rightarrow4^{-}}f\left(x\right)=1$, $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$, $\lim_{x\rightarrow4}f\left(x\right)=1$
• B. $\lim_{x\rightarrow4^{-}}f\left(x\right)=3$, $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$, $\lim_{x\rightarrow4}f\left(x\right)=3$
• C. $\lim_{x\rightarrow4^{-}}f\left(x\right)=3$, $\lim_{x\rightarrow4^{+}}f\left(x\right)=1$, $\lim_{x\rightarrow4}f\left(x\right)=DNE$
• D. $\lim_{x\rightarrow4^{-}}f\left(x\right)=1$, $\lim_{x\rightarrow4^{+}}f\left(x\right)=3$, $\lim_{x\rightarrow4}f\left(x\right)=DNE$

Find the specified limit or state that the limit does not exist by creating a table of values.

$f\left(x\right)=\frac{1}{x}$

$\lim_{x\rightarrow1^{-}}f\left(x\right)$, $\lim_{x\rightarrow1^{+}}f\left(x\right)$, $\lim_{x\rightarrow1}f\left(x\right)$

• A. $\lim_{x\rightarrow1^{-}}f\left(x\right)=0$, $\lim_{x\rightarrow1^{+}}f\left(x\right)=0$, $\lim_{x\rightarrow1}f\left(x\right)=1$
• B. $\lim_{x\rightarrow1^{-}}f\left(x\right)=1$, $\lim_{x\rightarrow1^{+}}f\left(x\right)=1$, $\lim_{x\rightarrow1}f\left(x\right)=1$$\lim_{x\rightarrow x}f\left(x\right)=1$
• C. $\lim_{x\rightarrow1^{-}}f\left(x\right)=1$, $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$, $\lim_{x\rightarrow1}f\left(x\right)=DNE$
• D. $\lim_{x\rightarrow1^{-}}f\left(x\right)=-1$, $\lim_{x\rightarrow1^{+}}f\left(x\right)=-1$, $\lim_{x\rightarrow1}f\left(x\right)=-1$

Cases Where Limits Do Not Exist

We just learned that if a function does not approach the same value from both sides, then the limit does not exist. But this is actually not the only scenario in which your limit won't exist. So here, I'm going to show you all possible cases that you may encounter in which your limit does not exist. So let's go ahead and not waste any time here and jump right into these limits. Now the first limit that we're asked to find here is the limit of f(x) as x approaches 3.

Now this function might look familiar and as we approach 3 getting really, really close from that left side, my function is going to a y-value of 1. Whereas from the right side, getting really, really close to 3, it's going to a y-value of 4. Because these are not the same from either side, we know that this limit does not exist. Now this won't happen for every piecewise function, but it does happen commonly for piecewise functions that have a jump like we see here. We have a jump in between one piece transitioning to the next one.

Now this is not the only case in which your limit won't exist, so let's go ahead and move on to our next limit here. Here we want to find the limit of f(x) as x approaches 2. Now as we get really, really close to 2 from either side, my function appears to be going to infinity. Now if both sides are going to infinity as x approaches 2, wouldn't that just be my limit? Well, no.

Here the limit does not exist because anytime that we have unbounded behavior, meaning that our function is going to infinity or negative infinity as x approaches c, our limit does not exist because infinity is not a number. So this happens commonly for rational functions that have an asymptote. And here we do have an asymptote right at x=2. So this is causing our unbounded behavior off to infinity, meaning that our limit does not exist. Now as you continue on in math, you may informally state the limit is equal to positive or negative infinity, but this is just used to describe the behavior of a function.

And for our purposes here anytime you see unbounded behavior as x approaches c your limit does not exist. Now let's move on to finding our final limit here. Here we want to find the limit of f(x) as x approaches 0. Now looking at our graph as we get really, really close to 0 from either side, our function appears to be doing something kind of crazy. It appears to be going up and down repeatedly.

It's oscillating. Now something that you may be thinking here is couldn't I just zoom in really, really far to my graph to see exactly what it's doing as x approaches 0? And the answer is no because the further and further that we zoom in here, the more and more you'll see this function oscillating. So here, for the limit of this function as x approaches 0, the limit actually does not exist. And this will be true of any function that is oscillating near c like we see here.

Now, this will happen often for functions that look exactly like this one, the sine of 1 over x or the cosine of 1 over x. So anytime you see a function like that, watch out for a limit that does not exist. Now that we know all the cases for which limits do not exist, let's continue practicing. Thanks for watching, and I'll see you in the next one.

Cases Where Limits Do Not Exist Example 2

Now that we know all of the cases for which a limit might not exist, let's go ahead and work through this example together. Feel free to try this on your own and then check back in with me. In this problem, we are asked to use the graph to estimate the value of each limit, or otherwise state that it does not exist. The first limit that we're asked to find here is the limit of \( f(x) \) as \( x \) approaches negative 2. So, looking at our graph here, as my x-value approaches negative 2 from the left side, getting really, really close to negative 2, I see that my function seems to be approaching a value of 0.

Then, coming in from the right side, getting really, really close to negative 2, I see again that my function seems to be approaching a value of 0. So, the limit of \( f(x) \) as \( x \) approaches negative 2 is equal to 0. Here, we also discern a piecewise function, but remember that in examining limits, we are evaluating values very close to the specific \( x \)-value. Therefore, even though other parts of the function exhibit different behavior, we focus solely near \( x = -2 \), thus, the limit exists and is 0.

Next, we're asked to find the limit of \( f(x) \) as \( x \) approaches 0. On our graph, as \( x \) approaches 0 from the left side, I see my function is approaching a value of 1. Similarly, coming in from the right side, as \( x \) approaches 0, the function continues to approach 1. Therefore, the limit of \( f(x) \) as \( x \) approaches 0 is 1. Even with a discontinuity at \( x = 0 \), this doesn't affect the limit because it's defined by the behavior as \( x \) gets really close to 0, not at 0 itself.

Lastly, we're tasked with finding the limit of \( f(x) \) as \( x \) approaches negative 3. Observing the graph, as \( x \) approaches negative 3 from the left, the function approaches a value of 1. However, from the right side, it's clear that the behavior is drastically different — the function displays unbounded behavior descending towards negative infinity. Here, because the one-sided limits do not agree and since one side exhibits unbounded behavior, the limit of \( f(x) \) as \( x \) approaches negative 3 does not exist.

If you have any questions, please feel free to ask. Let's continue on with some practice problems. I'll see you in the next video.

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).

$\lim_{x\rarr1}f\left(x\right)$

• A. $0$
• B. $1$
• C. $2$
• D. DNE

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).

$\lim_{x\rarr-2}f\left(x\right)$

• A. $-3$
• B. $1$
• C. $4$
• D. DNE

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).

$\lim_{x\rarr0}f\left(x\right)$

• A. $0$
• B. $1$
• C. $5$
• D. DNE

Use the graph of $f\left(x\right)$ to estimate the value of the limit or state that it does not exist (DNE).

$\lim_{x\rarr0}f\left(x\right)$

• A. $-1$
• B. $0$
• C. $1$
• D. DNE