Table of contents
- 1. Introduction to Biology2h 42m
- 2. Chemistry3h 40m
- 3. Water1h 26m
- 4. Biomolecules2h 23m
- 5. Cell Components2h 26m
- 6. The Membrane2h 31m
- 7. Energy and Metabolism2h 0m
- 8. Respiration2h 40m
- 9. Photosynthesis2h 49m
- 10. Cell Signaling59m
- 11. Cell Division2h 47m
- 12. Meiosis2h 0m
- 13. Mendelian Genetics4h 44m
- Introduction to Mendel's Experiments7m
- Genotype vs. Phenotype17m
- Punnett Squares13m
- Mendel's Experiments26m
- Mendel's Laws18m
- Monohybrid Crosses19m
- Test Crosses14m
- Dihybrid Crosses20m
- Punnett Square Probability26m
- Incomplete Dominance vs. Codominance20m
- Epistasis7m
- Non-Mendelian Genetics12m
- Pedigrees6m
- Autosomal Inheritance21m
- Sex-Linked Inheritance43m
- X-Inactivation9m
- 14. DNA Synthesis2h 27m
- 15. Gene Expression3h 20m
- 16. Regulation of Expression3h 31m
- Introduction to Regulation of Gene Expression13m
- Prokaryotic Gene Regulation via Operons27m
- The Lac Operon21m
- Glucose's Impact on Lac Operon25m
- The Trp Operon20m
- Review of the Lac Operon & Trp Operon11m
- Introduction to Eukaryotic Gene Regulation9m
- Eukaryotic Chromatin Modifications16m
- Eukaryotic Transcriptional Control22m
- Eukaryotic Post-Transcriptional Regulation28m
- Eukaryotic Post-Translational Regulation13m
- 17. Viruses37m
- 18. Biotechnology2h 58m
- 19. Genomics17m
- 20. Development1h 5m
- 21. Evolution3h 1m
- 22. Evolution of Populations3h 52m
- 23. Speciation1h 37m
- 24. History of Life on Earth2h 6m
- 25. Phylogeny2h 31m
- 26. Prokaryotes4h 59m
- 27. Protists1h 12m
- 28. Plants1h 22m
- 29. Fungi36m
- 30. Overview of Animals34m
- 31. Invertebrates1h 2m
- 32. Vertebrates50m
- 33. Plant Anatomy1h 3m
- 34. Vascular Plant Transport1h 2m
- 35. Soil37m
- 36. Plant Reproduction47m
- 37. Plant Sensation and Response1h 9m
- 38. Animal Form and Function1h 19m
- 39. Digestive System1h 10m
- 40. Circulatory System1h 57m
- 41. Immune System1h 12m
- 42. Osmoregulation and Excretion50m
- 43. Endocrine System1h 4m
- 44. Animal Reproduction1h 2m
- 45. Nervous System1h 55m
- 46. Sensory Systems46m
- 47. Muscle Systems23m
- 48. Ecology3h 11m
- Introduction to Ecology20m
- Biogeography14m
- Earth's Climate Patterns50m
- Introduction to Terrestrial Biomes10m
- Terrestrial Biomes: Near Equator13m
- Terrestrial Biomes: Temperate Regions10m
- Terrestrial Biomes: Northern Regions15m
- Introduction to Aquatic Biomes27m
- Freshwater Aquatic Biomes14m
- Marine Aquatic Biomes13m
- 49. Animal Behavior28m
- 50. Population Ecology3h 41m
- Introduction to Population Ecology28m
- Population Sampling Methods23m
- Life History12m
- Population Demography17m
- Factors Limiting Population Growth14m
- Introduction to Population Growth Models22m
- Linear Population Growth6m
- Exponential Population Growth29m
- Logistic Population Growth32m
- r/K Selection10m
- The Human Population22m
- 51. Community Ecology2h 46m
- Introduction to Community Ecology2m
- Introduction to Community Interactions9m
- Community Interactions: Competition (-/-)38m
- Community Interactions: Exploitation (+/-)23m
- Community Interactions: Mutualism (+/+) & Commensalism (+/0)9m
- Community Structure35m
- Community Dynamics26m
- Geographic Impact on Communities21m
- 52. Ecosystems2h 36m
- 53. Conservation Biology24m
20. Development
Developmental Biology
Problem 9`
Textbook Question
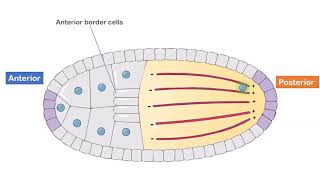
Imagine a situation in which a morphogen has its source at the posterior end of a Drosophila embryo. Every 100 µm from the posterior pole, the morphogen concentration decreases by half. If a cell required 1/16th the amount of morphogen found at the posterior pole to form part of a leg, how far from the posterior pole would the leg form?
a. 100 μm
b. 160 μm
c. 400 μm
d. 1600 μm
 Verified step by step guidance
Verified step by step guidance1
Understand the concept of morphogen gradient: A morphogen is a substance that defines different cell fates in a concentration-dependent manner. In this problem, the morphogen concentration decreases by half every 100 µm from the posterior pole of the Drosophila embryo.
Identify the initial concentration at the posterior pole: Let's denote the initial concentration of the morphogen at the posterior pole as C₀.
Determine the concentration required for leg formation: The cell requires 1/16th of the initial concentration (C₀) to form part of a leg. Therefore, the required concentration is C₀/16.
Calculate the distance where the concentration is C₀/16: Since the concentration halves every 100 µm, we can express the concentration at a distance x as C₀/(2^(x/100)). Set this equal to C₀/16 and solve for x using the equation:
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mfrac>
<mrow>
<msub>
<mi>C</mi>
<mn>0</mn>
</msub>
</mrow>
<mrow>
<msup>
<mn>2</mn>
<mfrac>
<mi>x</mi>
<mn>100</mn>
</mfrac>
</msup>
</mrow>
</mfrac>
<mo>=</mo>
<mfrac>
<msub>
<mi>C</mi>
<mn>0</mn>
</msub>
<mn>16</mn>
</mfrac>
</math>
Solve the equation for x: Simplify the equation to find the value of x that satisfies the condition. This involves solving the equation
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msup>
<mn>2</mn>
<mfrac>
<mi>x</mi>
<mn>100</mn>
</mfrac>
</msup>
<mo>=</mo>
<mn>16</mn>
</math>
which can be solved by recognizing that 16 is 2 raised to the power of 4, thus x/100 = 4, leading to x = 400 µm.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Morphogen Gradient
A morphogen gradient is a concentration gradient of a signaling molecule, known as a morphogen, which helps determine the fate of cells in a developing embryo. Cells interpret different concentrations of morphogens to activate specific developmental pathways. In this scenario, the morphogen concentration decreases by half every 100 µm from the posterior end, creating a gradient that influences cell differentiation.
Recommended video:
Guided course
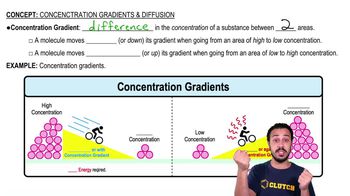
Concentration Gradients and Diffusion
Exponential Decay
Exponential decay describes a process where a quantity decreases at a rate proportional to its current value. In the context of the morphogen gradient, the concentration halves every 100 µm, indicating an exponential decay pattern. Understanding this concept is crucial for calculating the distance at which the morphogen concentration reaches a specific fraction of its initial value.
Recommended video:
Guided course

Exponential Population Growth
Logarithmic Calculation
Logarithmic calculation is used to solve problems involving exponential changes, such as determining the distance at which a morphogen concentration reaches a specific fraction of its initial value. By applying the properties of logarithms, one can calculate the number of halving events needed to reach 1/16th of the initial concentration, which corresponds to the distance from the morphogen source.
Recommended video:
Guided course

Mark & Recapture: Calculations & Assumptions

 5:28m
5:28mWatch next
Master Cell Division and Differentiation with a bite sized video explanation from Jason
Start learningRelated Videos
Related Practice




















![Drosophila Embryogenesis - Anterior/Posterior Patterning [English Captions]](https://img.youtube.com/vi/ZOzKXrOGtgw/mqdefault.jpg)