Calculating Vmax: Study with Video Lessons, Practice Problems & Examples

Theoretical maximal reaction velocity, or V_max, can be calculated using two primary methods: algebraic rearrangement of the Michaelis-Menten and Lineweaver-Burk equations, and through rate laws. The V_max is directly proportional to the product formation rate constant (k₂) and total enzyme concentration. Under saturating substrate concentrations, the initial reaction velocity (v₀) approaches V_max, allowing for substitutions in the rate law to derive V_max. Understanding these calculations is essential for analyzing enzyme kinetics effectively.

Calculating Vmax

In this video, we're going to begin our discussion on some of the tools that we have to calculate the theoretical maximal reaction velocity or the V_max. And so it turns out that the V_max can actually be calculated in multiple ways. And we're really going to talk about two primary ways to calculate the V_max. And so the first way that the V_max can be calculated is just by algebraic rearrangement. It can be calculated by algebraic rearrangement, specifically of the Michaelis-Menten or the Lineweaver-Burk equations. And so down below in our example, we're going to algebraically rearrange the Michaelis-Menten equation to solve for the V_max. And so notice down below what we have is the Michaelis-Menten equation right here on the left and on the right what we have is the Lineweaver-Burk equation. And so what we need to recall is that the Lineweaver-Burk equation is literally just the reciprocal of the Michaelis-Menten equation. And so that means that the relationship between the Michaelis-Menten and the Lineweaver-Burk equations is that they are reciprocals of one another. And so they can be pretty easily interconverted between each other. Essentially starting over here with the Michaelis-Menten equation, we can solve for the V_max. So we want to isolate and solve for this variable. And we can start off by essentially just moving this entire denominator here. And so what we can do is just move this denominator up into this side right here. And we can do that by multiplying both sides of our equation here by the denominator, Kilometers plus substrate concentration. And what that does is it gets rid of the denominator on the right side, so we're just left with the V_max times the substrate concentration on the right, and then on the left side, all we have is the initial reaction velocity times this denominator, so, essentially the initial reaction velocity times the Kilometers plus the substrate concentration. So now, again, we want to continue to isolate and solve for this V_max just like we're being asked to do in the example. And so what we can do is get rid of this substrate concentration by dividing both sides of the equation by the substrate concentration. Substrate concentration on the right. And of course, we're going to have the same expression that we had up above, so we're going to have the initial velocity times the Kilometers plus the substrate concentration on the top and all divided by the substrate concentration, that we needed to do to get rid of this on the right. And so what you can see here is we've algebraically rearranged the Michaelis-Menten equation to solve for the V_max, and so this is actually an expression that we can use to solve for the V_max in some of our practice problems. And so, essentially we'll be able to utilize some of this moving forward in our course. But in our next lesson video, we're going to talk about a second major way that we can use to calculate the V_max. So I'll see you guys in that video.

Calculating Vmax

So in addition to calculating the \( V_{max} \) through algebraic rearrangement of the Michaelis-Menten and the Lineweaver-Burk equations, we can also calculate the \( V_{max} \) through rate laws. And so what we need to recall from our previous lesson videos is that the \( V_{max} \) is actually directly proportional to both the product formation rate constant, which is \( k_2 \), and the total enzyme concentration. And so, we did cover this in some of our previous lesson videos. And so, recall that biochemists mainly focus on measuring and plotting the initial reaction velocity or the \( v_0 \) of enzyme-catalyzed reactions. And so we know that the initial reaction velocity or the \( v_0 \) is also expressed as the change in the concentration of product over the change in time. And so, because it's the product concentration that is relevant to biochemists, they actually focus on measuring the initial reaction velocity of the product formation step in our typical enzyme-catalyzed reaction. And so notice down below what we have is our typical enzyme-catalyzed reaction, and we know that this is the initial reaction because notice that the rate constant \( k_{-2} \) here is being ignored. It's negligible. So, catalyzed reaction, and notice that with this initial enzyme-catalyzed reaction. And notice that with this initial enzyme-catalyzed reaction, there's only one rate constant that affects the change in the product concentration, and that is the rate constant \( k_2 \). And so that's why biochemists are mainly focused on the product formation step of an enzyme-catalyzed reaction and the rate law for the product formation step. And so down below, what we have is the rate law for the product formation step. And so we know that the rate law is really just another way to express reaction velocities, and so it's going to be the rate law is going to be the initial reaction velocity, which is equal to the rate constant, which is going to be \( k_2 \) for the product formation step. So we can say it's equal to \( k_2 \), times the concentration of the reactant. And so for this product formation reaction right here, the reactant of this reaction is actually the enzyme substrate complex. So it's going to be times the concentration of the enzyme substrate complex, and then we know it's going to be raised to the power of the reaction order. And because this is a simple enzyme-catalyzed reaction, we know that the coefficient, which is essentially 1 here, is going to be the reaction order. So we can assume that it's a one and so what we're saying is that it's this expression right here that is the rate law for the product formation step. And again, this is all review information from our previous lesson video, so no new information in this video. And so, the next thing that we need to recall from our previous lesson videos is that this initial reaction velocity, so this initial reaction velocity \( v_0 \), is really the velocity that has the best chance at approaching the theoretical maximal velocity \( V_{max} \). And again, that's what we're interested in calculating in this video, is the \( V_{max} \). And so what we can say is that there is this possibility of variable substitution where we can substitute the initial reaction velocity \( V_0 \) with the \( V_{max} \). And that's exactly what we're going to do with this rate law down below. So, recall that under saturating substrate concentrations, we can actually take the initial reaction velocity in the rate law for the product formation step and substitute it with the \( V_{max} \). And so that's exactly what we've done here, substituted the initial reaction velocity with the \( V_{max} \). And also recall that under saturating substrate concentrations, all of the enzyme, the total enzyme concentration, is going to be associated with the substrate. There's so much substrate because it's saturating. And so that means that the total enzyme concentration is going to approximately equal the concentration of the enzyme substrate complex. And so what that means is we can take the enzyme substrate complex here and substitute it with the total enzyme concentration. And so that's exactly what we're doing here. We're substituting the concentration of the enzyme substrate complex with the total enzyme concentration. And of course, this rate law here is still going to be the rate law for the product formation step, so it's still going to be \( k_2 \) here. And so, essentially, what we're going to do is to be \( k_2 \) here. And so, essentially, what we're saying is that this here is another way to calculate the \( V_{max} \) of a reaction, through this rate law. And so moving forward with our practice problems, we're going to need to identify which of the two methods do we need to use to calculate the \( V_{max} \). And so we'll be able to get some practice making these decisions and our practice problems. So I'll see you guys there.

Calculating Vmax Example 1

Alright. So here we have an example problem that wants us to calculate the maximum reaction velocity or V_max of an enzyme if the Michaelis constant (K_m) is equal to 7 millimolar and the initial reaction velocity or V₀ is equal to 86.71 micromolar per second when the substrate concentration is equal to 25 millimolar. And so in our previous lesson videos, we talked about two predominant ways of calculating the maximum reaction velocity (V_max). Of these two ways, we can see that in this problem we are neither given the product formation rate constant (k₂) nor the total enzyme concentration, which means that we are not going to be able to use this method here to calculate the V_max, and that means that we are going to need to algebraically rearrange the Michaelis-Menten equation to solve for the V_max. So, recall from our previous lesson videos that we can do that by multiplying both sides of the equation by the denominator to move it up here, and then dividing both sides of the equation by the substrate concentration to move that away over here so that V_max is all by itself.

When we do that we end up with an equation that says that V_max is going to be equal to the initial reaction velocity times the Michaelis constant plus the substrate concentration, all divided by the substrate concentration. Essentially, all we need to do to calculate the V_max in this problem is to plug in the values that we have for these variables. However, what we need to note is that these variables here are in different units. The K_m is in units of millimolar, the substrate concentration is also in units of millimolar, but the initial reaction velocity is in units of micromolar per second. And all of our answer options have units of molarity. So what this means is we might as well convert all of these units of concentration into units of molarity so that it matches one of our answer options. We need to do that first before we try plugging in the values into our expression.

If we take this initial reaction velocity of 86.71 micromolar, per second, and converting this micromolar into molarity so that it matches our answer option. We know that there are 10⁶ micromolar in 1 molarity. So, all we need to do is to divide 86.71 by 10⁶, and we'll get an answer of 8.671 × 10^-5=, and this is going to be in units of molarity. Now that we've converted units of molarity, we can bring back in the seconds that we had before.

For the K_m, which is equal to 7 millimolar, we want to convert that into molarity so that they're all matching the units. There are 1,000 millimolar in 1 molar, which allows our unit to cancel. So if we divide 7 by 1,000, we'll get the answer of 0.007 molar. This is our new K_m. Lastly, we have our substrate concentration, which is 25 millimolar, so again we want to convert that into units of molarity. There are 1,000 millimolar in 1 molar, so dividing 25 by 1,000 is equal to 0.025 molar.

All our units match now, we can plug in these values into our expression over here. Rewriting, we'll have:

V_max = V₀ × (K_m + substrate concentration) / substrate concentration

V max = V o × k m + [S] ÷ [S]

Plugging in values:

V max = 8.671 × 10 - 5 0.007 + 0.025 0.025

After calculating the above expression, the V_max is found to be approximately 1.11 × 10^-4 M/s. This matches with answer option C. Therefore, option C here is the correct answer for this problem.

That concludes our example here, so I'll see you guys in our practice problems where we can get more practice applying these concepts.

Suppose an enzyme (MW = 5,000 g/mole) has a concentration of 0.05 mg/L. If the k_cat is 1 x 10⁴ s^-1, what is the theoretical maximum reaction velocity for the enzyme?

• A. 1050 µM/s.
• B. 100 µM/s.
• C. 150 µM/s.
• D. 105 µM/s.

For a Michaelis-Menten enzyme, what is the value of V_max if at 1/10 Km, the V₀ = 1 μmol/min.

• A. 1.5 μmol/min.
• B. 11 μmol/min.
• C. 19 μmol/min.
• D. 103 μmol/min.
• E. μmol/min.

Carbonic anhydrase catalyzes the hydration of CO₂. The Km of carbonic anhydrase for CO₂ is 12 mM. The initial velocity (V₀) of the enzyme-catalyzed reaction was 4.5 μmole*mL^-1*sec^-1 when [CO₂] = 36 mM. Calculate the V_max of carbonic anhydrase.

• A. 8.1 x 10² M s^-1.
• B. 6 x 10^-3 M s^-1.
• C. 2.5 x 10^-4 M s^-1.
• D. 7.3 x 10^-5 M s^-1.

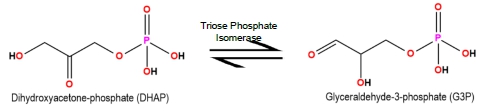
Triose phosphate isomerase catalyzes the conversion of dihydroxyacetone phosphate (DHAP) to glyceraldehyde-3-phosphate (G3P) during glycolysis; however, this is a reversible reaction. The K_m of the enzyme for G3P is 1.8 x 10 ^-5 M. When [G3P] = 30 μM, the initial rate of the reaction (V₀) = 82.5 μmole*mL^-1*sec^-1. Calculate the V_max.

• A. 0.493 M s^-1.
• B. 1.201 M s^-1.
• C. 0.067 M s^-1.
• D. 0.132 M s^-1.

Here’s what students ask on this topic:

What is Vmax in enzyme kinetics?

Vmax, or the theoretical maximal reaction velocity, represents the maximum rate at which an enzyme can catalyze a reaction when the substrate concentration is saturating. It is a crucial parameter in enzyme kinetics, indicating the enzyme's catalytic efficiency. Vmax is achieved when all enzyme active sites are occupied by the substrate, meaning the enzyme is working at its full capacity. Understanding Vmax helps in determining the enzyme's efficiency and its potential in various biochemical reactions.

How can Vmax be calculated using the Michaelis-Menten equation?

Vmax can be calculated by algebraically rearranging the Michaelis-Menten equation. The Michaelis-Menten equation is given by:

$\frac{V=V{\max }_{}\cdot S}{K{m}_{}+S}$

To solve for Vmax, isolate it on one side of the equation:

$V\cdot (K{m}_{}+S)=V{\max }_{}\cdot S$

Then, divide both sides by the substrate concentration (S):

$\frac{V\cdot (K{m}_{}+S)}{S}=V{\max }_{}$

This rearranged equation can be used to calculate Vmax from experimental data.

What is the Lineweaver-Burk equation and how is it used to determine Vmax?

The Lineweaver-Burk equation is the double reciprocal form of the Michaelis-Menten equation. It is given by:

$\frac{1}{V}=\frac{K{m}_{}}{V{\max }_{}\cdot S}+\frac{1}{V{\max }_{}}$

By plotting 1/V against 1/[S], a straight line is obtained where the y-intercept is 1/Vmax and the slope is Km/Vmax. This linear transformation allows for easier determination of Vmax and Km from experimental data.

How does substrate concentration affect the calculation of Vmax?

Substrate concentration plays a crucial role in the calculation of Vmax. Under saturating substrate conditions, the enzyme's active sites are fully occupied, and the reaction rate approaches Vmax. This allows for accurate determination of Vmax. If the substrate concentration is not saturating, the reaction rate will be lower, and Vmax cannot be accurately determined. Therefore, experiments to calculate Vmax should be conducted under conditions where the substrate concentration is high enough to ensure that the enzyme is working at its maximum capacity.

What is the relationship between Vmax and enzyme concentration?

Vmax is directly proportional to the total enzyme concentration. This means that if the enzyme concentration is doubled, the Vmax will also double, assuming that the substrate concentration is saturating. The relationship can be expressed as:

$V{\max }_{}=k{\mathrm{cat}}_{}\cdot E{t}_{}$

where k_cat is the turnover number (the number of substrate molecules converted to product per enzyme molecule per unit time) and E_t is the total enzyme concentration. This relationship highlights the importance of enzyme concentration in determining the maximum reaction velocity.