- 1. Chemical Measurements1h 50m
- 2. Tools of the Trade1h 17m
- 3. Experimental Error1h 52m
- 4 & 5. Statistics, Quality Assurance and Calibration Methods1h 57m
- 6. Chemical Equilibrium3h 41m
- 7. Activity and the Systematic Treatment of Equilibrium1h 0m
- 8. Monoprotic Acid-Base Equilibria1h 53m
- 9. Polyprotic Acid-Base Equilibria2h 17m
- 10. Acid-Base Titrations2h 37m
- 11. EDTA Titrations1h 34m
- 12. Advanced Topics in Equilibrium1h 16m
- 13. Fundamentals of Electrochemistry2h 19m
- 14. Electrodes and Potentiometry41m
- 15. Redox Titrations1h 14m
- 16. Electroanalytical Techniques57m
- 17. Fundamentals of Spectrophotometry50m
Hypothesis Testing (t-Test): Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AIThe t-test is a statistical method used to compare the means of populations, particularly when the population standard deviation is unknown. The t-score is calculated using the formula:
The t-Test is used to measure the similarities and differences between two populations.
The t-test
t-Test
Video transcript
t-Test Calculations
Video transcript
So here it states, a student wishing to calculate the amount of arsenic in cigarettes decides to run 2 separate methods in her analysis. The results shown in parts per million are shown below. Alright, so we have 5 samples for both methods. Here it asks us, is there a significant difference between the 2 analytical methods under a 95% confidence interval? All right.
We're dealing with confidence intervals. We know we're going to be dealing with t calculated in some way. Realize here that we're not dealing with just one method with a set of measurements, so we can't just simply use our t score formula to find t calculated and compare it to our t table. Because we're dealing with 2 different methods with their own set of samples, we're going to have to rely on the t test. Now the t test, basically we're going to say here if our t calculated which is what we're going to figure out is greater than our t table, we're going to say that there is a significant difference in terms of the means for these two different methods.
If we calculate t and we see that it is less than our t table, then we will say there is no significant difference. Now how do we figure out t calculated? Remember from the previous page, when it comes to our t test, t calculated can be determined in 3 different ways. Either by figuring out we have equal variances and therefore we'd use those set of equations. We have unequal variances so we'd use a different set of equations or if we have paired data in which we use yet another set of equations.
Here they're talking about 2 separate methods. So 2 different runs under different situation, therefore this isn't paired data. That means we have to determine are the variances in these two methods, are they equal or are they non-equal? Determining that will determine which formula we use for t calculated and for our standard deviations or our degrees of freedom. We have to figure out what their variances are.
Remember, variance is just your standard deviation squared. We're going to say here, we first have to figure out what our means are for each. For method 1, we're going to say that our mean or average equals each one of the measurements divided by the total number of measurements divided by 5. So when we do that, that gives us 92.1 for the mean or average of our first method. For the second method, we do the same thing again.
Add up each one of the measurements divided by the total number of measurements. Divide by 5. This equals 92.06. All right. Now that we've determined that, we're going to now find the standard deviations of the 2.
From that information, we'll be able to determine are they equal or not equal? That will determine which set of equations we should use to figure out t calculated. Now we're going to need room guys so let me take myself out of the image. Let's look at method 1. Now remember from previous videos that standard deviation which we're just going to label as s equals square root and we have the summation of each measurement minus the average or mean squared divided by number of measurements minus 1.
For method 1, standard deviation equals 1 equals 110.5 minus the average that we found for method 1 squared. Next measurement, 93.1 minus 92.1 squared. 63.0 minus 92.1 squared plus 72.3 minus 92.1 squared. And then finally, 121.6-92.1 squared divided by n minus 1. n is the number of measurements which is 5 minus 1.
Here when we do all that, we get a standard deviation of 24.742. Next, method 2. Its standard deviation, same exact process. So here we have 104.7 minus 92.06 squared plus 95.8 minus 92.06 squared plus 71.2-92.1 squared oh, actually, 92.06 squared plus 69.9 minus 92.06 squared. And then finally, plus 118.7 minus 92.06 squared divided by number of measurements which is 5 minus 1.
Here when we do that, our standard deviation comes out to 21.27. Remember, your variance is just your standard deviation squared. It would just be 24.742 squared. So here when we do that, we get a value of 612.167 and then 21.27 squared equals 452.413. Here we have our variances for both.
We can see that they are They're very much different values. Okay. We'd say here that the variances are not equal to one another. And because the variances are not equal to one another, that tells us which formula to use to figure out my t calculated. We're going to say unequal variances.
Variances that are equal to one another really are different by less than 1 from one another. Here, they're different by, well over a 100 from another. We know that we're dealing with unequal variances. Now we're going to use the formula to figure out t calculated when the variances are not equal. t calculated when the variances are not equal equals x, so average or mean of method 1 minus average or mean of method 2 in absolute brackets, divided by square root of standard deviation 1 squared divided by n 1 plus standard deviation 2 squared divided by n 2.
So that's our formula that we're going to use to figure out t calculated. All we do now is we input the values that we got. So that's 92.1 minus 92.06 divided by 24.742 squared divided by 5 plus okay. And we're taking the square root of this part right here. And this is gonna be 21.27 squared divided by 5 equals alright.
So now we're gonna say this top portion up here is 0.04. For the bottom portion, let's plug in these values here and figure out what number we're gonna get, And then we'll see what our t calculated comes out to being. So here, plugging all that in. Okay. So that'll be squared.
So we have that portion right there. So this right here comes out to being 122.433. And then this portion here comes out to being +90.4826 equals. So let's see when we plug that in, what that gives us. That comes out to being 0.002741 from my t calculated.
We have to double-check our numbers. That's our t calculated for right now. Now we are going to have to compare that t calculated to our t table value. But remember, we know that we're dealing with a 95% confidence interval. We know what percentage we're dealing with but we still can't use the t table yet because we are also missing our degrees of freedom.
Now associated with this t calculated when the variance is not equal, is also our formula for degrees of freedom. This can be kind of complicated so degrees of freedom, When we have unequal variances is this equation. So it's a it's a pretty big equation. Again, you're not gonna be expected to memorize this. You'd be given this, on a formula sheet so don't freak out too much by the length of this equation.
So here our degrees of freedom would be here. It'd be standard deviation 1 squared divided by the measurements for method 1 plus standard deviation 2 squared divided by number of measurements for method 2. So this is all squared divided by standard deviation 1 squared divided by measurements. This is squared divided by number of measurements from method 1 minus 1 plus standard deviation 2 squared divided by number of measurements from method 2 squared divided by number of measurements for method 1 minus 1. You can see that it's a huge, big mess of numbers.
Now, if you do this correctly, what you should get for the top portion when you plug all this in and you take the square, you should get 45333.2 divided by and then the bottom portion, we'd get here 3747.48 when we do this portion, plus 246.77 when we do this portion here, And then that comes out to 7.8 or roughly 8.0. Remember, our degrees of freedom needs to be a whole number. So we just round up to 8.0. Now go back a few pages. Look at the t table.
We have 84 degrees of freedom. We have a 95% confidence interval we're looking at. Make those numbers meet up. If you look at it correctly, you'll see that the t value according to our t table equals 2.306. That's our t table value.
Now, we come up here and remember the 2 conditions, whether t table is greater than or less than t calculated. We found out that t table was 2.306 and then we saw that our t calculated is this value here, 0.002743. Okay. So then here, I think that was the number right. 02741.
Yes. Alright. So we can see here that our t table value is a bigger number than our t calculated value. What does that mean? That means that there is no significant difference in the means between the two methods or our two populations in this case.
Remember, for a question like this when they're talking about 2 sets of data, they each represent a population. We're going to require the t test in order to test the means between those two populations. We had to first figure out what our averages were for both and from that, we'd be able to determine their standard deviations. From these standard deviations, you can calculate your variances. If the variances are unequal, we did this method to find our answer.
If the variances had been equal, then we would have used the other set of values to find t calculated, our s pooled and our degrees of freedom, and then still compare it to our t table to see if there is a significant difference or not. Just remember the steps that we employed here. Remember the use of the t table as well as the formulas from the previous page whenever we're dealing with percent confidence intervals and the t test.
t-Test Calculations
Video transcript
So in this question, it states that you want to determine if concentrations of hydrocarbons in seawater measured by fluorescence are significantly different than concentrations measured by a second method specifically based on the use of gas chromatography/flame ionization detection, which is labeled as GCFID. You measure the concentrations of a certified standard reference material which is 100.0 micromolar. In both methods, you have 7 times. Specifically, you first measure each sample by fluorescence and then measure the same sample by GCFID. The concentrations determined by the 2 methods are shown below.
Alright. So, we have these 7 samples being measured by 2 completely different methods. And we know that because we're using 2 entirely different methods, which we're then going to compare to one another, we know that this is a paired data test. It's paired data. That tells us what formula we need to use to figure out our standard deviation as well as our t calculated value.
Here it says calculate the appropriate t statistic to compare the 2 sets of measurements. Right. So again, we're looking at 2 entirely different methods in order to figure out these values. And because they're totally different methods, we're going to compare them by the paired data steps. We're going to say here following paired data, t c a l c u l a t e d = m e a n d i f f e r e n c e s t a n d a r d d e v i a t i o n × n . Then we're going to say our standard deviation equals ∑ ( d i f f e r e n c e - m e a n d i f f e r e n c e ) 2 n − 1 . Now how do we figure out our difference? Well, here, we're going to come up with another column, which is our difference. So what we're going to do here is we're going to take each one of these numbers and subtract them from each other.
This is 100.2 minus 101.2 which equals negative 0.9.
Then we're gonna do 100.9 minus 100.5, which gives me negative 0.3, and so on for the rest of the values. All we've just done is figure out the differences by subtracting these values from one another. Alright, now that we have that, we're going to have to figure out what our mean difference is. Just like any mean, we're gonna take each one of the differences, add them together, and divide by the number of measurements.
It's going to be negative 0.9 + 0.4 + negative 0.3 + negative 0.1 + 0.3 + 0.4 + 0.1 divided by the number of measurements, which is 7. When we do that, that's going to give me negative 0.014 as my mean difference. Next, we're going to do our standard deviation. Here, standard deviation, you're going to take each difference minus the mean difference squared and then sum them up and divide by the number of measurements minus 1. So you can see that this is very tedious, but you gotta make sure you plug them in correctly. Divided by the number of measurements, which is 7 minus 1, is how we calculate our standard deviation as 0.47.
Now that we have that, we can figure out what our t calculated is. T calculated here equals again the mean difference, in absolute terms, divided by standard deviation times the square root of the number of measurements. That equals 0.014 0.47 × 7 .
Again, we're dealing with these 7 measurements here. Here, when we do that, we get our t calculated as 0.08. Here, let's assume that we're dealing with a 95% confidence interval because that's quite the common percentage to look at. Here, our t calculated, again, is 0.08. All you gotta do is go back to your student's t table.
Here, we have to figure out our degrees of freedom. Your degrees of freedom, which I'll abbreviate as DOF, is N minus 1. The number of measurements from the differences is 7 minus 1, giving a degree of freedom of 6. Look at your student's t table, look for degrees of freedom of 6, then move over to the right and look for a 95% confidence interval. See where they meet. They meet where t table would equal 2.447.
We're going to say here that t calculated is less than T table. Because of that, even though we used 2 separate methods, we're going to say that there doesn't appear to be any significant difference between both methods. Whether you're using fluorescence or GCFID, either method more or less gives us similar means for the 2 sample populations. Again, we used paired data here because we're dealing with analyzing populations by 2 different methods. One was the fluorescence method, and the other one was GCFID. When we're using completely different methods, we rely on the paired data approach. If the methods are different, and we're testing 2 populations, then we have to look to see if their variances are equal or not.
Determining if their variances are equal or not helps to determine which set of equations to use to figure out t calculated, standard deviation, and your degrees of freedom.
t-Test Calculations
Video transcript
In this question, it says a sample of size
Remember, we said that if we're going above 30, that usually means that we're not using the t-test but instead the z-test. Now, because I don't give you a
If you line up infinity with your 95% confidence interval, you'll see that your
Look at the similarities that this has with a typical confidence interval. A typical confidence interval would just be the mean plus or minus your
Our mean here is 16 plus or minus 1.960 times your deviation which is 3 divided by the square root of 100. Here, when we plug all this into our calculator, it gives us 0.588. So this is 16 plus or minus 0.588. What does that mean? That means we have 16 minus 0.588 and then we have 16 plus 0.588.
So, that means that we're 95% confident that our value will lie between 15.412 to 16.588. That would be our level of confidence within this particular question. Remember, when we're going beyond 30, we transition from more of a
Once you do, come back and see how I approach that same exact practice question.
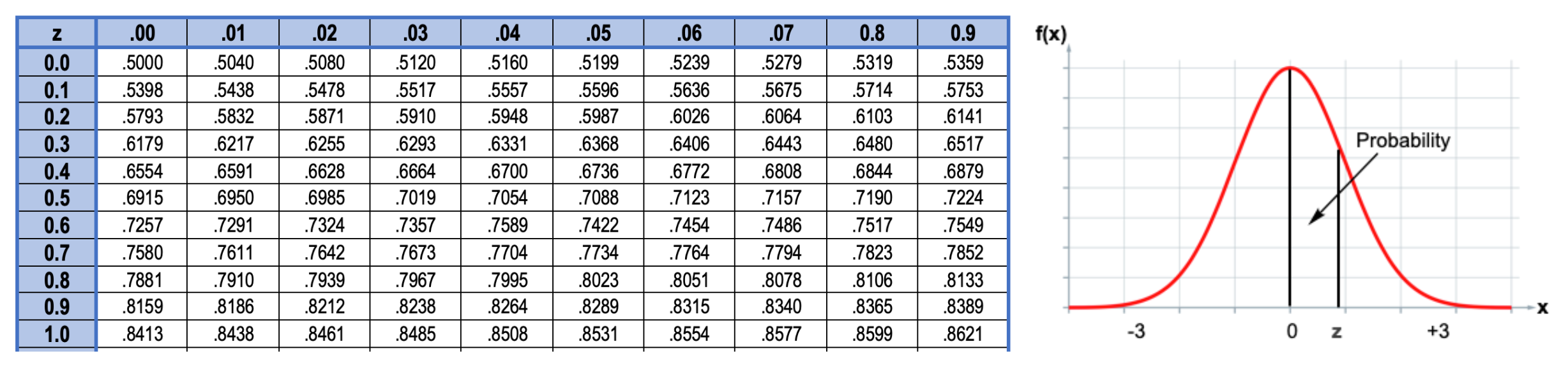
The average height of the US male is approximately 68 inches. What is the probability of selecting a group of males with average height of 72 inches or greater with a standard deviation of 5 inches?

Here’s what students ask on this topic:
What is the t-test used for in statistics?
The t-test is a statistical method used to compare the means of two populations, especially when the population standard deviation is unknown. It helps determine if there is a significant difference between the means of the populations. The t-score is calculated using the formula:
A larger t-score indicates greater differences between the populations. Variations of the t-test include equal variance, unequal variance, and paired data, each requiring specific calculations to determine significant differences using a t-table.
 Created using AI
Created using AIWhen should you use a t-test instead of a z-test?
You should use a t-test instead of a z-test when the population standard deviation is unknown and the sample size is less than 30. The t-test is more appropriate in these cases because it accounts for the additional uncertainty in the estimate of the population standard deviation. The t-test uses the sample standard deviation (s) and adjusts for smaller sample sizes, making it more reliable for small samples. In contrast, the z-test is used when the population standard deviation is known and the sample size is large (typically n > 30).
 Created using AI
Created using AIHow do you interpret the t-score in a t-test?
The t-score in a t-test indicates how much the sample mean deviates from the population mean in units of the standard error. A larger t-score suggests a greater difference between the sample and population means. To interpret the t-score, you compare it to a critical value from the t-table, which depends on the degrees of freedom and the desired confidence level. If the t-score is greater than the critical value, it indicates a significant difference between the means. If it is less, there is no significant difference.
 Created using AI
Created using AIWhat are the different types of t-tests and when are they used?
There are three main types of t-tests: independent t-test (equal variance), independent t-test (unequal variance), and paired t-test. The independent t-test (equal variance) is used when comparing the means of two independent groups with equal variances. The independent t-test (unequal variance) is used when the variances of the two groups are not equal. The paired t-test is used when comparing means from the same group at different times or under different conditions. Each type of t-test has specific formulas and considerations for calculating the t-score and degrees of freedom.
 Created using AI
Created using AIWhat is the formula for calculating the t-score in a t-test?
The formula for calculating the t-score in a t-test is:
where
 Created using AI
Created using AI