Analysis of Variance (f-Test): Study with Video Lessons, Practice Problems & Examples

The F-test is utilized to compare the variances of two populations, calculated as the ratio of their squared standard deviations. Always place the larger standard deviation in the numerator to ensure the F-calculated value is ≥ 1. If F-calculated < F-table, variances are equal; if F-calculated > F-table, variances are unequal. This affects the formulas for t-calculated and degrees of freedom, which are essential for hypothesis testing in statistics.

F-Test

So when we're dealing with the F-test, remember the F-test is used to test the variance of 2 populations, and remember that variance is just your standard deviation squared. Now, we're going to say F calculated represents the quotient of the squares of the standard deviations. Here it is standard deviation 1 squared divided by standard deviation 2 squared. We're going to say when calculating our F quotient, so basically this value, always set the largest standard deviation as the numerator, so that way F calculated will always be equal to or greater than 1. Now, we're gonna say here we can compare our F calculated value to our F table value to determine if there is a significant difference based on the variances.

Here we're going to say if your F calculated is less than your F table, then the difference will not be significant. So here we'd say that they would have equal variances. As a result, our t calculated and s pooled formulas would be these 2 here. Here x one is just the measurements, the mean or average of your first measurements minus the mean or average of your second measurements divided by s pooled, and it's just the number of measurements. So population 1 has this set of measurements, population 2 has its own set of measurements.

Here if your F calculated is greater than your F table, then there is a significant difference. So we're gonna say here you'd have unequal variances, which would mean that you'd use a different set of values. Here, this would be the equation to figure out t calculated and then this would be our formula to figure out your degrees of freedom. Remember we've seen these equations before in our exploration of the t-test, and here is our F table. So your degrees of freedom for standard deviation 1, which is the largest standard deviation, and these are your degrees of freedom for standard deviation 2.

Just like with the t-table, you just have to look to see where the values line up in order to figure out what your t table value would be, and then compare it to your F well figure out what your F table value would be and then compare it to your F calculated value. As we explore deeper and deeper into the F-test, you'll see how we use this particular chart with questions dealing with the F-test.

F-Test Calculations 1

In the process of assessing responsibility for an oil spill, 2 possible suspects are identified. To differentiate between the two samples of oil, the ratio of the concentration for 2 polyaromatic hydrocarbons is measured using fluorescent spectroscopy. These values are then compared to the sample obtained from the body of water. So we have information on our suspects and the sample we're testing them against. So we have the averages or mean, the standard deviations of each, and the number of samples of each.

Here we're asked if there is a concern that any combination of the standard deviation values demonstrates a significant difference. To determine this, we need to find out what the calculated F-value for each combination is, and if the calculated F-value happens to be greater than our F-table value, then there would be a significant difference. To do this, we first figure out our degrees of freedom for each sample, which are \( n - 1 \) where \( n \) is the number of samples.

This would be \(4 - 1\) which is 3, 4, and 5. We'll use that later on with this table here. Now to figure out our \( F \) calculated, we're going to say \( F \) calculated equals \( \frac{{\text{{standard deviation}}_1^2}}{{\text{{standard deviation}}_2^2}} \). Remember the larger standard deviation is what goes on top so that \( F \) calculated is always a number equal to or greater than 1. We are using different combinations, so I'll compare the first two to one another resulting in \(1.58829\). Next is \( \frac{{s_1^2}}{{s_2^2}} \). Now let's do this one and this one resulting in \(1.45318\). And for the last possible combination, \( \frac{{0.092^2}}{{0.088^2}} \), results in \(1.09298\).

Now these represent our \( F \) calculated values. All we have to do is compare them to the F-table values. The first standard deviation, \( s_1 \), has a degree of freedom of 4, and \( s_2 \) has a degree of freedom of 3. They give us an F-table value of \(9.12\). Since the \( F \) calculated value of \(1.58\) is less than the F-table value, there is no significant difference. Next, the standard deviation of \(0.088\) is associated with an F-table value of \(9.01\), where again the F-table is larger than the calculated F, indicating no significant difference. Finally, one has 4 degrees of freedom and the other 5, resulting in an F-table value of \(5.19\). In all three combinations, there is no significant difference because the calculated \( F \) is not larger than the F-table.

Since there is no significant difference, this will play a role in determining which formulas to use for example 2. You can attempt to do example 2 on your own based on there being no significant difference in their standard deviations. If you get lost and aren't sure what to do next, just click over to the next video and see how I approach example 2.

F-Test Calculations 1

So in example 2 it states, can either or both of these suspects be eliminated based on the results of the analysis at the 99% confidence interval? Now realize here because in example 1 we found out there was no significant difference in their standard deviations, that means we're dealing with equal variance. Because we are dealing with equal variance, this dictates which version of s_{\text{pooled}} and t_{\text{calculated}} formulas we'll have to use. Now since there's going to be a lot of numbers on the screen, I'll have to take myself out of the image for a few minutes. So let's look at suspect 1 and then we'll look at suspect 2 and we'll see if either one can be eliminated.

For suspect one, we're dealing with equal variance in both cases, so therefore s_{\text{pooled}} = \sqrt{s_1^2 \times (n_1 - 1) + s_2^2 \times (n_2 - 1)} / (n_1 + n_2 - 2) . Alright. So for suspect 1, we're comparing the information on suspect 1 to the sample itself. We'll be using the values from these two for suspect 1.

Let’s come back down here. And before we come back actually, we're going to say here because the sample itself. Alright. We can say here that, we'll make this one s_1 and we can make this one s_2 , but it really doesn't matter in the grand scheme of our calculations. So we come back down here, we'll plug in s_1 = 0.073^2 \times (4-1) + 0.088^2 \times (6-1) / (4+6-2) .

When we plug all that in that gives us \sqrt{0.006838} , and that comes out to 0.082694 for s_{\text{pooled}} . Now that we have s_{\text{pooled}} we can figure out what t_{\text{calculated}} would be. So t_{\text{calculated}} , because we have equal variance, equals in absolute terms \frac{|x_1 - x_2|}{s_{\text{pooled}} \sqrt{\frac{n_1 \times n_2}{n_1 + n_2}}} . So the mean or average for the suspect one is 2.31 and for the sample 2.45. We've just found out what s_{\text{pooled}} was, so plug that in Times the number of measurements, so that's 4 \times 6 / (4+6) .

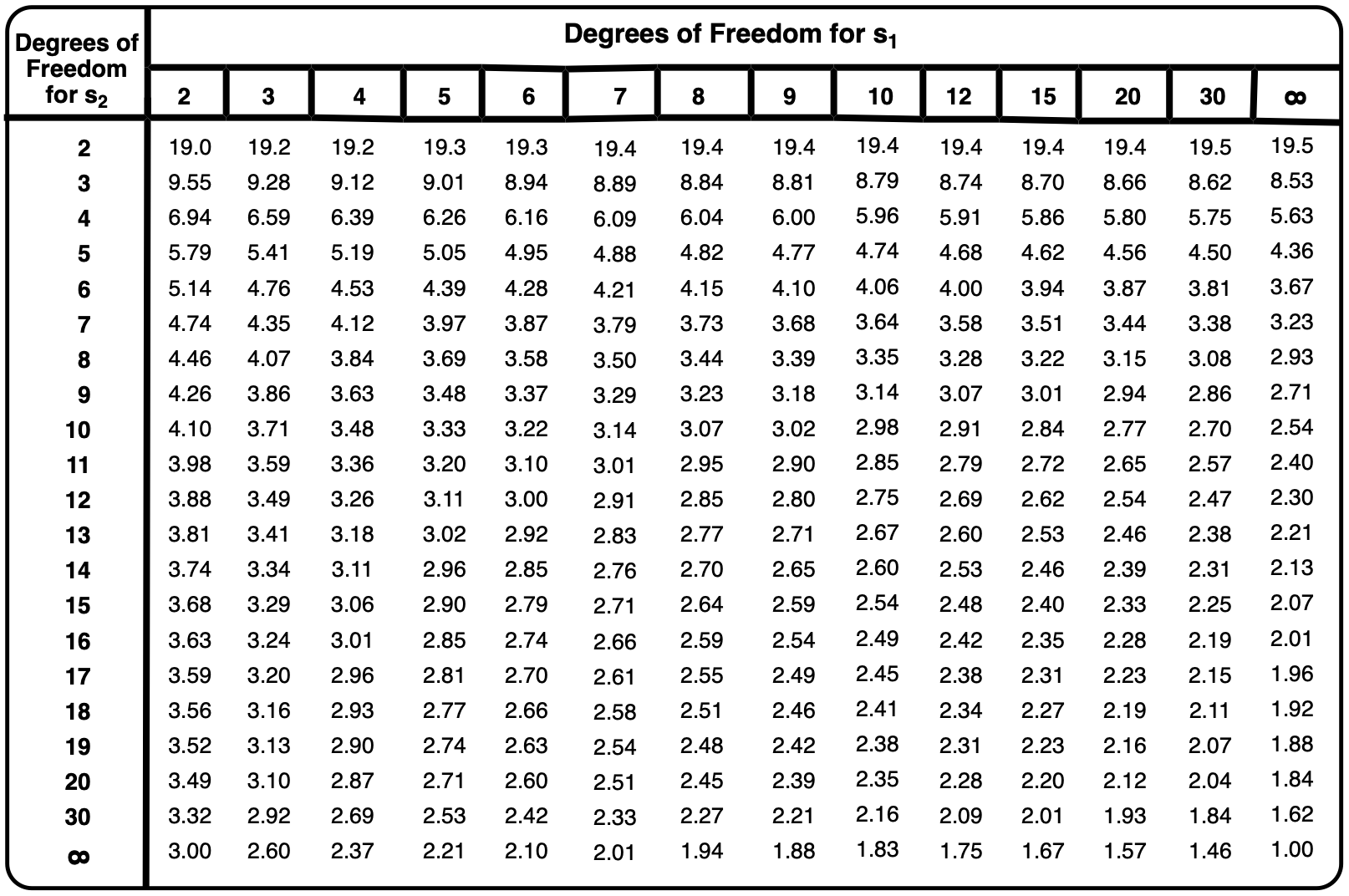
So all of that gives us 2.62277 for our t_{\text{calculated}} . Now, if t_{\text{calculated}} is larger than t_{\text{table}} , then there would be a significant difference between the suspect and the sample. Here, if you use a t table, our degrees of freedom are normally n - 1 , but in comparing the two to one another, my degrees of freedom now become this, n_1 + n_2 - 2 . So that would be 4 + 6 - 2, which gives me a degree of freedom of 8. If you go to your t table, look at 8 for the degrees of freedom, and then go all the way to the 99% confidence interval.

That gives us a t_{\text{table}} value equal to 3.355. So what is this telling us? Well, this is telling us that our t_{\text{calculated}} is not greater than our t_{\text{table}} . t_{\text{table}} is larger, so that means there is no significant difference between suspect 1 and the sample.

So that means suspect 1 could be guilty of the oil spill because t_{\text{calculated}} is less than t_{\text{table}} . There's no significant difference. Suspect 1 is a potential violator. Now let's look at suspect 2. So suspect 2 we're going to do the same thing.

s_{\text{pooled}} equals the same exact formula, but now we're using different values. We're comparing suspect 2 now to the sample itself. So suspect 2 has a standard deviation of 0.092, which we'll square times its number of measurements which is 5 minus 1, plus the standard deviation of the sample, and that's also squared. It had 6, 6 samples minus 1, divided by 5 + 6 minus 2. So here that gives us \sqrt{0.008064} .

So that equals 0.0898. Now that we have s_{\text{pooled}} we can find t_{\text{calculated}} here, which would be the same exact formula we used here. So here the mean of my suspect 2 is 2.67 minus 2.45 divided by my s_{\text{pooled}} , which we just found, times 5 times 6 divided by 5 + 6. So that's 2.44989 times 1.65145.

So t_{\text{calculated}} here equals 4.04586. My degrees of freedom would be 5 + 6 - 2, which is 9. So we look up 9 for our degrees of freedom, we go all the way to the 99% confidence interval, so t_{\text{table}} equals 3.250. So in this example t_{\text{calculated}} is greater than t_{\text{table}} . That means there is a significant difference between the sample and suspect 2, which means that they are innocent.

So in this example, which is like an everyday analytical situation, where you have to test crime scenes and in this case an oil spill to see who is truly responsible, we can see that suspect 1, there was no significant difference because t_{\text{calculated}} was not greater than t_{\text{table}} . So suspect 1 is responsible for the oil spill. Suspect 2, if t_{\text{calculated}} was greater than t_{\text{table}} , so there is a significant difference, therefore exonerating suspect 2. So again, if we had had unequal variance, we'd have to use a different combination of equations for s_{\text{pooled}} and t_{\text{calculated}} , and then compare t_{\text{calculated}} again to t_{\text{table}} . So, again, the F-test really is just looking to see if our variances are equal or not, and from there it can help us determine which set of equations to use in order to compare t_{\text{calculated}} to t_{\text{table}} .

F-Test Calculations 2

Here it says you are measuring the effects of a toxic compound on an enzyme. You expose five test tubes of cells to 100 microliters of a 5 parts per million aqueous solution of the toxic compound and mark them as treated. And expose five test tubes of cells to an equal volume of only water and mark them as untreated. You then measure the enzyme activity of cells in each test tube. Enzyme activity in this case is in units of micromoles per minute.

Here are the following other measurements of enzyme activity. We're given here two columns. We have our enzyme activity that's been treated and enzyme activity that's been untreated. We have five measurements for each one.

From this, we're able to obtain our average or mean for each one. We're also given our standard deviation. Now, this question asks, is the variance of the measured enzyme activity of cells exposed to the toxic compound equal to that of cells exposed to water alone. Alright, so we know that variance, if we're trying to compare the variance between two samples or two sets of samples, that means we're relying on the F test. What we have to do here is determine what the F calculated value will be.

Remember, F=s12/s22. 𝐒₁, the one on top is always the larger standard deviation. So that means that our 𝐅 calculated at the end must always be a value that is equal to or greater than 1. So here are our standard deviations for the treated and untreated. So, we always put the larger standard deviation on top again.

So, 0.362/0.292. When we do that calculation, it's going to give me 1.54102 as my 𝐅 calculated. What I do now is remember the previous page where we're dealing with 𝐅 tables, we have five measurements for both treated and untreated. And if we line them up perfectly, that means our 𝐅 table would be 5.05. All we do now is compare our 𝐅 table value to our 𝐅 calculated value.

So here, 𝐅 calculated is 1.54102. 𝐅 table is 5.05. If 𝐅 table is greater than 𝐅 calculated, that means we're going to have equal variance. So that just means that there is not a significant difference. So since there's not a significant difference, this will play a major role in what we do in example 2.

So work this example 2 out if you remember when your variances are equal, what set of formulas do we use. If you still can't quite remember how to do it or how to approach it, just click on to the next video and see how I answer example 2.

F-Test Calculations 2

Alright guys, because we had equal variance in example 1, that tells us which series of equations to use to answer example 2. Here it says is the average enzyme activity measured for cells exposed to the toxic compound significantly different at 95% confidence level, than that can be measured for cells exposed to water alone. Because we're going to have to utilize a few equations, I'm going to have to take myself out of the image guys but follow along. Again, we had equal variance according to example 1. That tells me that I have to use t calculated.

And we're going to use the version that is equal to absolute value of average 1 minus average 2 divided by spooled times square root of n1×n2 divided by N1+N2. And then here because we need S pooled, S pooled in this case would equal square root of standard deviation 12 times the number of measurements minus 1, plus standard deviation 22, number of measurements minus 1, divided by n1+n2 minus 2. Now, we're used to seeing the degrees of freedom as being n minus 1, but because here we're using 2 sets of data, our new degrees of freedom actually becomes n1+n2 minus 2. All right. Now all we have to do is plug in the values to get our t calculated.

All right. So let's first figure out what our s pooled will be. So equals. So up above, we said that our standard deviation 1 which is the largest standard deviation is 0.36. That'll be squared.

Number of measurements is 5 minus 1 plus smaller deviation is s2.29 squared, 5 minus 1 divided by 5+5 minus 2. So when we take when we figure out everything inside, that gives me square root of 0.10685. Taking the square root of that gives me an s pooled equal to 0.32679. So that's my s pooled. So that's going to go here in my formula.

So here t calculated equals 3.84 minus 6.15 from up above in absolute terms, divided by s pooled, which we calculated as 0.32679 times 5 times 5 divided by 5+5. So that gives me 7.06684 times 1.58114. Multiplying them together, I get a t calculated that is 11.1737. Now we have to determine if they're significantly different at a 95% confidence level. So here we need to figure out what our t table is.

So if you take out your t tables, we'd say that our degrees of freedom remember, our degrees of freedom would normally be n minus 1, but when dealing with the f test here, the degrees of freedom actually become this, n1+n2. So that's 5+5-two, so that's going to be a degree of freedom of 8. And we look at degree of freedom of 8, we look at the 95% confidence interval, so my ttabled value equals 2.306. So now we compare ttable to tcalculated. So we're going to say here that tcalculated is 11.1737, which is greater than ttable, which is 2.306.

Because of this, because t calculated is greater than t table, that means we have to reject the measurements as being significantly different. So we're going to say, yes, significantly different between the 2 based on a 95% confidence interval or confidence level. Now, if we had gotten variances that were not equal, remember we use another set of equations to figure out what our t calculator would be and then compare it between that and the t table to determine if there would be any significant difference between my treated samples and my untreated samples. Remember, when it comes to the F test, it's just a way of us comparing the variances of 2 datasets, and seeing if there's significant differences between them. Here, in terms of confidence intervals or confidence levels, we then enter into the realm of looking at t calculated versus t table to find our final answer.

Here’s what students ask on this topic:

What is the purpose of the F-test in statistics?

The F-test is used in statistics to compare the variances of two populations. It helps determine if there is a significant difference between the variances of the two groups. This is done by calculating the ratio of their squared standard deviations, known as the F-calculated value. By comparing the F-calculated value to the F-table value, we can conclude whether the variances are equal or unequal. If F-calculated is less than F-table, the variances are considered equal; if F-calculated is greater than F-table, the variances are unequal. This test is essential for hypothesis testing and helps in making informed decisions based on statistical data.

How do you calculate the F value in an F-test?

To calculate the F value in an F-test, you need the standard deviations of two populations. The formula for the F value is:

$\frac{s^1}{s^2}$

where $s^1$ is the standard deviation of the first population and $s^2$ is the standard deviation of the second population. Always place the larger standard deviation in the numerator to ensure the F-calculated value is ≥ 1. Once you have the F-calculated value, compare it to the F-table value to determine if the variances are significantly different.

What is the significance of comparing F-calculated to F-table in an F-test?

Comparing F-calculated to F-table in an F-test is crucial for determining whether the variances of two populations are significantly different. The F-table value is a critical value obtained from statistical tables based on the degrees of freedom for each population. If F-calculated is less than F-table, it indicates that the variances are not significantly different, meaning they are equal. Conversely, if F-calculated is greater than F-table, it suggests that the variances are significantly different, meaning they are unequal. This comparison helps in hypothesis testing and making informed decisions based on the data.

How do you determine the degrees of freedom for an F-test?

The degrees of freedom for an F-test are determined based on the sample sizes of the two populations. For the numerator (the larger standard deviation), the degrees of freedom are calculated as $n-1$, where $n$ is the sample size of the first population. For the denominator (the smaller standard deviation), the degrees of freedom are calculated similarly as $n-1$, where $n$ is the sample size of the second population. These degrees of freedom are then used to find the critical F-table value for comparison with the F-calculated value.

What are the implications of having unequal variances in an F-test?

Having unequal variances in an F-test implies that the variability within the two populations is significantly different. This affects the formulas used for further statistical analysis, such as calculating the t-value and degrees of freedom for a t-test. When variances are unequal, different formulas are used to account for this discrepancy, ensuring accurate hypothesis testing. Unequal variances can indicate that the populations are not homogeneous, which may impact the reliability of statistical inferences drawn from the data. Therefore, identifying and accounting for unequal variances is crucial in statistical analysis.